
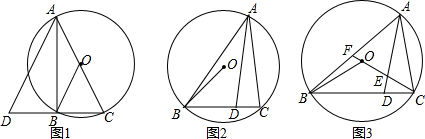
���� ��1����AC��ֱ��֪AB��CD��������AD=AC�����ݵ������������ʿɵá�DAC=2��BAC=2��ABO��
��2����AD=AC�á�1=��C������֪��2=2��C=��1+��C�����ɡ�2+��ABO+��3=��1+��C+��DAC=180��á�DAC=��3+��ABO=2��ABO������DAC=2��ABO��
��3���ӳ�CO����O�ڵ�G����BG������B��BN��FG������C��CM��AB����tan��BFN=tan��AFC=$\frac{5\sqrt{3}}{3}$֪$\frac{BN}{NF}=\frac{5\sqrt{3}}{3}$������BN=5$\sqrt{3}$a��NF=3a�����ݹ��ɶ����ɵ�BF������Rt��BNG��֪GN=5a�����ݵȱ�����������֪ON=5a����뾶OG=10a��GF=8a������֪CF=12a����Rt��CFM�пɵ�FM=$\frac{6\sqrt{21}}{7}$a��CM=$\frac{30\sqrt{7}}{7}$����Rt��ACM�пɵ�AC=AD=$\frac{20\sqrt{21}}{7}a$��AM=$\frac{10\sqrt{21}}{7}$a�������õ�AF=$\frac{16\sqrt{21}}{7}$a��֤��AFC=��AEF��AF=AE������AD-AE=DE�г�����a�ķ��̣��ⷽ�̿ɵ�aֵ���ɵð뾶10a��ֵ��
��� �⣺��1����AC����Բ��O��
��AC��ֱ����
���ABC=90�㣬
��AB��CD��
�֡�AD=AC��
��ABƽ�֡�DAC��
���DAC=2��BAC��
��OA=OB��
���OAB=��ABO��
���DAC=2��ABO��
��2��������Ȼ����
�������£���ͼ2������AO ��AD=AC��
��AD=AC��
���1=��C��
�ߡ�2�͡�C�ǻ�AB���Ե�Բ�ĽǺ�Բ�ܽ�
���2=2��C=��1+��C��
��OA=OB��
���ABO=��3��
�ߡ�2+��ABO+��3=��1+��C+��DAC=180��
���DAC=��3+��ABO=2��ABO
����DAC=2��ABO��
��3����ͼ3���ӳ�CO����O�ڵ�G����BG������B��BN��FG�ڵ�N������C��CM��AB�ڵ�M��
�ߡ�BOC=120�㣬
���BOG=180��-120��=60�㣬
�֡�OG=OB��
���OGB�ǵȱ������Σ�
���G=60�㣬GN=ON��
�ߡ�AFC=��BFN��
����Rt��BNF��tan��BFN=tan��AFC=$\frac{5\sqrt{3}}{3}$��
��$\frac{BN}{NF}=\frac{5\sqrt{3}}{3}$��
��BN=5$\sqrt{3}$a����NF=3a��
��BF=$\sqrt{B{N}^{2}+N{F}^{2}}$=2$\sqrt{21}$a��
��Rt��BNG�У�GN=5a����ôON=5a��
��뾶OG=OB=OC=5a+5a=10a��GF=GN+NF=8a��
��CF=CG-GF=2��10a-8a=12a
��Rt��CFM�У���CMF=90�㣬tan��AFC=$\frac{5\sqrt{3}}{3}$��
��FM=$\frac{6\sqrt{21}}{7}$a��CM=$\frac{30\sqrt{7}}{7}$a��
�ߡ�BAC=$\frac{1}{2}$��BOC=$\frac{1}{2}$��120��=60��
��Rt��ACM�У��ɵ�AC=AD=$\frac{20\sqrt{21}}{7}a$��AM=$\frac{10\sqrt{21}}{7}$a��
��AF=AM+FM=$\frac{6\sqrt{21}}{7}$a+$\frac{10\sqrt{21}}{7}$a=$\frac{16\sqrt{21}}{7}$a��
�֡ߡ�AEF=��ACE+��DAC=��ABG+��DAC=��ABG+2��ABO=��OBG+��ABO=60��+��ABO��
�ߡ�AFC=��BOF+��ABO=60��+��ABO��
���AFC=��AEF
��AF=AE��
��AD-AE=DE��
��$\frac{20\sqrt{21}}{7}$a-$\frac{16\sqrt{21}}{7}$a=2����ã�a=$\frac{\sqrt{21}}{6}$��
��뾶OC=10a=10��$\frac{\sqrt{21}}{6}$=$\frac{5\sqrt{21}}{3}$��
���� ������Ҫ�������Ǻ������ȱ��������ж������ʡ������ε��ڽǡ���Ƕ�����Բ�ܽǶ�����֪ʶ�㣬�ۺ���ǿ���������Ǻ�������ֱ��������Ϊ����㣬��ʾ����ͬ�߶γ�����ת�Ƶ�Բ�İ뾶�����ǹؼ����ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ����x��y�ύ�ڵ�A��1��0����B��0��-1���뷴��������y=$\frac{m}{x}$�ڵ�һ�����ڵ�ͼ���ڵ�C����C��������Ϊ1��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��0����ͼ����x��y�ύ�ڵ�A��1��0����B��0��-1���뷴��������y=$\frac{m}{x}$�ڵ�һ�����ڵ�ͼ���ڵ�C����C��������Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=a4 | B�� | a6��a3=a2 | C�� | a3��a2=a5 | D�� | ��a3b��2=a5b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
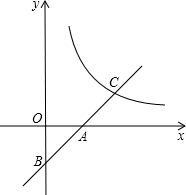
 ��ͼ����O����AB��뾶OC�ཻ�ڵ�P��BC��OA����C=50�㣬��ô��APC�Ķ���Ϊ75�㣮
��ͼ����O����AB��뾶OC�ཻ�ڵ�P��BC��OA����C=50�㣬��ô��APC�Ķ���Ϊ75�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
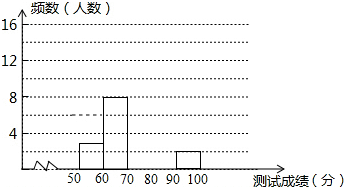 Ϊ����ǿѧ��������ʶ��ijУ�ٰ����조���ɽ�У�����������С�֪ʶ��������ѡ�κ���25��ѧ���μӾ�������25��ѧ��ͬʱ���50��ѡ���⣬��ÿ��ȷһ��ѡ�����2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
Ϊ����ǿѧ��������ʶ��ijУ�ٰ����조���ɽ�У�����������С�֪ʶ��������ѡ�κ���25��ѧ���μӾ�������25��ѧ��ͬʱ���50��ѡ���⣬��ÿ��ȷһ��ѡ�����2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����| ��� | �ɼ�x�� | Ƶ���������� |
| ��1�� | 50��x��60 | 3 |
| ��2�� | 60��x��70 | 7 |
| ��3�� | 70��x��80 | 10 |
| ��4�� | 80��x��90 | m |
| ��5�� | 90��x��100 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
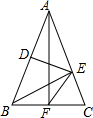 ��ͼ����ABC�У�AB=AC��DE��ֱƽ��AB��BE��AC��AF��BC����������۴�����ǣ�������
��ͼ����ABC�У�AB=AC��DE��ֱƽ��AB��BE��AC��AF��BC����������۴�����ǣ�������| A�� | BF=EF | B�� | DE=EF | C�� | ��EFC=45�� | D�� | ��BEF=��CBE |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ÿ��С�����εı߳���Ϊ1�ķ���ֽ�У����߶�AB���߶�DE����A��B��D��E����С�����εĶ����ϣ�
��ͼ����ÿ��С�����εı߳���Ϊ1�ķ���ֽ�У����߶�AB���߶�DE����A��B��D��E����С�����εĶ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com