
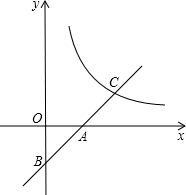
 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,-1)与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点C,点C的纵坐标为1.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,-1)与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点C,点C的纵坐标为1.分析 (1)根据一次函数y=kx+b(k≠0)的图象与x、y轴交于点A(1,0),B(0,-1),可以求得k、b的值,从而可以得到一次函数的解析式;
(2)根据一次函数y=x-1与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点C,点C的纵坐标为1,可以求得点C的坐标,进而可以求得m的值,从而可以得到反比例函数的解析式.
解答 解:(1)∵点A(1,0),B(0,-1)在一次函数y=kx+b的图象上,
∴$\left\{\begin{array}{l}{k+b=0}\\{b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
即一次函数的解析式为y=x-1;
(2)∵一次函数y=x-1与反比例函数y=$\frac{m}{x}$在第一象限内的图象交于点C,点C的纵坐标为1,
∴将y=1代入y=x-1得,x=2,
∴点C的坐标为(2,1),
∴1=$\frac{m}{2}$,
解得m=2,
即点C的坐标是(2,1),反比例函数的解析式是$y=\frac{2}{x}$.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,找出所求问题需要的条件.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
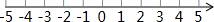 利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.
利用数轴,解一元一次不等式组:$\left\{\begin{array}{l}{x+4≤3(x+2)}\\{\frac{x-1}{2}<\frac{x}{3}}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
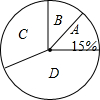 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com