
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
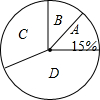 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
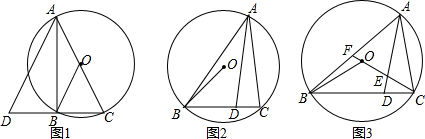
 如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com