
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.分析 (1)根据比例设出每天包装大黄米5m千克,江米4m千克,由两种米每天包装总数为45千克可得出关于m的一元一次方程,解方程即可得出结论;
(2)设出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式,结合图象分段利用待定系数法求出函数解析式;
(3)算出每种米每千克的利润,结合(2)的关系式可列出关于x的一元一次不等式,解不等式即可得出结论.
解答 解:(1)设平时每天包装大黄米5m千克,则每天包装江米4m千克,
根据题意可知:5m+4m=45,
解得:m=5,
5m=5×5=25,
4m=4×5=20.
答:平时每天包装大黄米25千克,每天包装江米20千克.
(2)设这20天内每天包装大黄米的质量随天数变化的函数关系式为y1=k1x+b1,每天包装江米的质量随天数变化的函数关系式为y2=k2x+b2,
当0≤x<15时,有$\left\{\begin{array}{l}{25={b}_{1}}\\{40=15{k}_{1}+{b}_{1}}\end{array}\right.$和$\left\{\begin{array}{l}{20={b}_{2}}\\{38=15{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=1}\\{{b}_{1}=25}\end{array}\right.$和$\left\{\begin{array}{l}{{k}_{2}=1.2}\\{{b}_{2}=20}\end{array}\right.$.
即y1=x+25,为y2=1.2x+20;
当15≤x≤20时,有$\left\{\begin{array}{l}{40=15{k}_{1}+{b}_{1}}\\{25=20{k}_{1}+{b}_{1}}\end{array}\right.$和$\left\{\begin{array}{l}{38=15{k}_{2}+{b}_{2}}\\{20=20{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-3}\\{{b}_{1}=85}\end{array}\right.$和$\left\{\begin{array}{l}{{k}_{2}=-3.6}\\{{b}_{2}=92}\end{array}\right.$.
即y1=-3x+85,为y2=-3.6x+92.
综上可知:每天包装大黄米的质量随天数变化的函数关系式为y1=$\left\{\begin{array}{l}{x+25(0≤x<15)}\\{-3x+85(15≤x≤20)}\end{array}\right.$,
每天包装江米的质量随天数变化的函数关系式为y2=$\left\{\begin{array}{l}{1.2x+20(0≤x<15)}\\{-3.6x+92(15≤x≤20)}\end{array}\right.$.
(3)大黄米每千克的利润为10-0.5-7.9=1.6(元);江米每千克的利润为12-9.5-0.5=2(元).
当0≤x<15时,每天销售大黄米和江米的利润之和1.6×(x+25)+2×(1.2x+20)=4x+80,
令4x+80>120,解得:10<x<15;
当15≤x≤20时,每天销售大黄米和江米的利润之和1.6×(-3x+85)+2×(-3.6x+92)=-12x+320,
令-12x+320>120,解得:15≤x≤16.
故在这20天中从第11 6天销售大黄米和江米的利润之和大于120元.
点评 本题考查了待定系数法求函数解析式、解一元一次不等式以及解一元一次方程,解题的关键是:(1)利用比例设出未知数,列出方程;(2)利用待定系数法求函数解析式;(3)列出关于x的一元一次不等式.本题属于中档题型,(1)(3)难度不大,(2)有些难度,由于函数图象是折线故需分段考虑函数解析式.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | k>-$\frac{1}{3}$ | B. | k>$\frac{1}{3}$ | C. | k<-$\frac{1}{3}$ | D. | k<$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
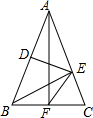 如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下面结论错误的是( )
如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则下面结论错误的是( )| A. | BF=EF | B. | DE=EF | C. | ∠EFC=45° | D. | ∠BEF=∠CBE |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.
如图,在平面直角坐标系中,直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公点,若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象没有公共点,则b的取值范围是-2<b<2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
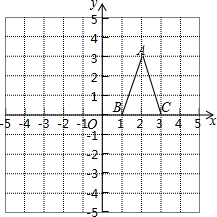 如图△ABC在直角坐标系中:
如图△ABC在直角坐标系中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com