
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)6、15、24、33.(2)∠AOM﹣∠NOC=30°,理由见解析
【解析】
试题分析:(1)根据已知条件可知,在第t秒时,三角板转过的角度为10°t,然后按照OA、OC、ON三条射线构成相等的角分四种情况讨论,即可求出t的值;
(2)根据三角板∠MON=90°可求出∠AOM、∠NOC和∠AON的关系,然后两角相加即可求出二者之间的数量关系.
解:(1)∵三角板绕点O按每秒10°的速度沿逆时针方向旋转,
∴第t秒时,三角板转过的角度为10°t,
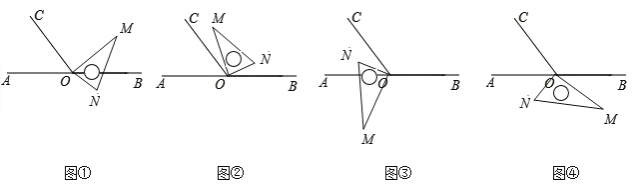
当三角板转到如图①所示时,∠AON=∠CON
∵∠AON=90°+10°t,∠CON=∠BOC+∠BON=120°+90°﹣10°t=210°﹣10°t
∴90°+10°t=210°﹣10°t
即t=6;
当三角板转到如图②所示时,∠AOC=∠CON=180°﹣120°=60°
∵∠CON=∠BOC﹣∠BON=120°﹣(10°t﹣90°)=210°﹣10°t
∴210°﹣10°t=60°
即t=15;
当三角板转到如图③所示时,∠AON=∠CON=![]() ,
,
∵∠CON=∠BON﹣∠BOC=(10°t﹣90°)﹣120°=10°t﹣210°
∴10°t﹣210°=30°
即t=24;
当三角板转到如图④所示时,∠AON=∠AOC=60°
∵∠AON=10°t﹣180°﹣90°=10°t﹣270°
∴10°t﹣270°=60°
即t=33.
故t的值为6、15、24、33.
(2)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON,∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树(如图)的高度,设计的方案及测量数据如下:

(1)在大树前的平地上选择一点A,测得由点A看大树顶端C的仰角为35°;
(2)在点A和大树之间选择一点B(A,B,D在同一直线上),测得由点B看大树顶端C的仰角恰好为45°;
(3)量出A,B两点间的距离为4.5米.
请你根据以上数据求出大树CD的高度.(精确到0.1米)(可能用到的参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OB平分∠CBA,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=18,则△AMN的周长为( )

A.30 B.33 C.36 D.39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种童装,平均每天可售出20件,每件盈利40元。经市场调查发现,若每件降价1元,则平均每天可多售2件。该商场要保证每天盈利1200元,同时又使顾客得到实惠,那么每件应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取资讯的主要渠道,设置“A:手机,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,则该调查的方式是_______.(填普查或抽样调查)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去 B.带②去 C.带③去 D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
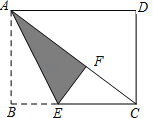
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
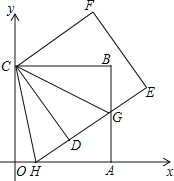
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com