
����Ŀ��ij�ľ����۵����������г�ѡ��A��B�����ľߣ�������A��Ϊ12Ԫ/����B��Ϊ8Ԫ/�������õ�����A��B�����ľߵ���������y�����������ۼ�x��Ԫ/��������һ�κ�����ϵ������ͼ��
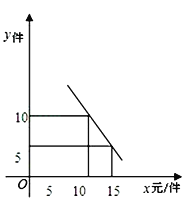
��1����y��x�ĺ�����ϵʽ��
��2���õ�ƻ����ѡ��A��B�����ľߵ�������100���������ʽ���1000Ԫ����ϣ��ȫ���������������296Ԫ������A���ľ�ÿ���ɻ���4Ԫ��B���ľ�ÿ���ɻ���2Ԫ���㣬��õ�������ļ��ֽ���������
��3����A���ľߵ����ۼ۱�B���ľߵ����ۼ۸�2Ԫ/�����������ľ�ÿ�����������W��Ԫ����A���ľ����ۼ�x��Ԫ/����֮��ĺ�����ϵʽ����˵��A��B�����ľ����ۼ۷ֱ�Ϊ����ʱ��ÿ�����۵��������
���𰸡���1��y=-x+20����2�������ֽ�����������A��48����B��52������A��49����B��51������A��50����B��50������3����A���ľ����ۼ�Ϊ16Ԫ/����B���ľ����ۼ�Ϊ14Ԫ/��ʱ��ÿ�����۵��������
�������������������1����y=kx+b���ѵ㣨10,10������15,5�����룬Ȼ��ⷽ���鼴�ɣ���2������ι���A���ľ�a����Ȼ����ݹ�ϵ�������ʽ���1000Ԫ����ϣ��ȫ���������������296Ԫ���в���ʽ���ȷ��x��ȡֵ��Χ��Ȼ��ȷ�������⼴�ɣ���3�����w��z�ĺ�����ϵʽ��Ȼ����ݶ��κ���������������������ֵ���ɣ�
����������⣺��1����y=kx+b����![]() ��
��
���![]() ��
��
��y��x�ĺ�����ϵʽΪy=-x+20��
��y=4������ʱ��x=16��Ԫ������A���ľ�ÿ������16-12=4��Ԫ����
����ι���A���ľ�a������B���ľߣ�100-a������
��![]() �����48��a��50��
�����48��a��50��
��a��������a=48��49��50��
������������ֽ�����������A��48����B��52������A��49����B��51������A��50����B��50����
��3���������W=��x-12����-x+20��+��x-2-8��[-��x-2��+20]��
��W=-2x2+64x-460=-2��x-16��2+52��
����A���ľ����ۼ�Ϊ16Ԫ/����B���ľ����ۼ�Ϊ14Ԫ/��ʱ��ÿ�����۵��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ��ѱ�ʾ3�ĵ��������������ƶ�5����λ�������λ�����Ӧ������ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��չ�ô�μ���������Ϊ20Ԫ������͵���Ϊ80Ԫ������100����
��1���蹺��������Ϊx��������������������ܷ���Ϊy��Ԫ��������д��y��x�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2�����������������ܷ��ò�����6620Ԫ��������������������������3������ô���ļ��ֹ�����
��3���ӽ�Լ��֧�ĽǶ�����������Ϊ�������ַ��������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ1����ABCD����ABC=60o���߳�Ϊ3�������������ȱ������Ρ�AEF���߳�Ϊ![]() ����E����F���ֱ���AB��AC�ϣ���AΪ��ת���Ľ���AEF˳ʱ��ת������ת��Ϊ������ͼ2.
����E����F���ֱ���AB��AC�ϣ���AΪ��ת���Ľ���AEF˳ʱ��ת������ת��Ϊ������ͼ2.
��1����ͼ2��֤��BE=CF��
��2������BAE=45o����CF�ij�����
��3����CF=![]() ʱ��ֱ��д����ת�����Ķ�����
ʱ��ֱ��д����ת�����Ķ�����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�DZ�����һ�ֲ�Ʒ30�������ͼ��Ʒ��������y����λ��������ʱ��t����λ���죩�Ĵ��º�����ϵ��ͼ�٣�ͼ����һ����Ʒ����������z����λ��Ԫ����ʱ��t����λ���죩�ĺ�����ϵ����֪����������=����������һ����Ʒ�������������н����������ǣ� ��
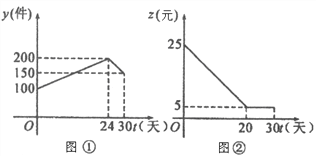
A. ��������Ϊ150�����ǵ�12�����30��
B. ��10������һ����Ʒ��������15Ԫ
C. �ӵ�1�쵽��20�����ʱ���������������������ټ���
D. ��18���������������1225Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. x2+x2��2x4 B. x2x3��x6 C. ��x2��3��x6 D. ��2x2��3��6x6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com