
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(﹣3,3),过点A的直线y=![]() x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
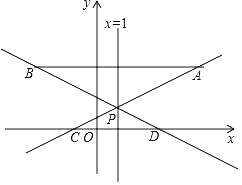
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
科目:初中数学 来源: 题型:
【题目】第33个国际禁毒日到来之际,贵阳市策划了以“健康人生绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
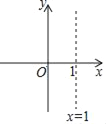
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,2×2网格(每个小正方形的边长为1)中有A,B,C,D,E,F,G,H,O九个格点.抛物线l的解析式为y=(-1)nx2+bx+c(n为整数).

(1)n为奇数,且l经过点H(0,1)和C(2,1),求b,c的值,并直接写出哪个格点是该抛物线上的顶点;
(2)n为偶数,且l经过点A(1, 0)和B(2,0),通过计算说明点F(0,2)和H(0,1)是否在抛物线上;
(3)若l经过这九个格点中的三个,直接写出满足这样条件的抛物线条数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段,下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
跳远(米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
跳绳(次) | 63 |
| 75 | 60 | 63 | 72 | 70 |
|
| 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A.5号学生进入30秒跳绳决赛
B.2号学生进入30秒跳绳决赛
C.8号学生进入30秒跳绳决赛
D.9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:初中数学 来源: 题型:
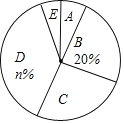
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上的信息,回答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %.
(2)被调查学生的总数为 人,统计表中m的值为 ,统计图中n的值为 .
(3)在统计图中,E类所对应扇形圆心角的度数为 .
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在学习中遇到这样一个问题:
如图,点![]() 是弧
是弧![]() 上一动点,线段
上一动点,线段![]() 点
点![]() 是线段
是线段![]() 的中点,过点
的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .当
.当![]() 为等腰三角形时,求线段
为等腰三角形时,求线段![]() 的长度.
的长度.

小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:
![]() 根据点
根据点![]() 在弧
在弧![]() 上的不同位置,画出相应的图形,测量线段
上的不同位置,画出相应的图形,测量线段![]() 的长度,得到下表的几组对应值.
的长度,得到下表的几组对应值.
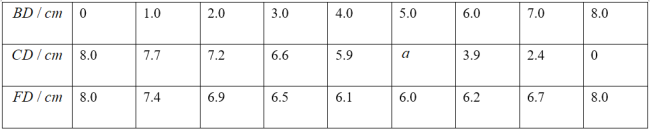
操作中发现:
①"当点![]() 为弧
为弧![]() 的中点时,
的中点时, ![]() ".则上中
".则上中![]() 的值是
的值是
②"线段![]() 的长度无需测量即可得到".请简要说明理由;
的长度无需测量即可得到".请简要说明理由;
![]() 将线段
将线段![]() 的长度作为自变量
的长度作为自变量![]() 和
和![]() 的长度都是
的长度都是![]() 的函数,分别记为
的函数,分别记为![]() 和
和![]() ,并在平面直角坐标系
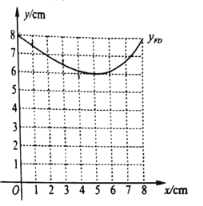
,并在平面直角坐标系![]() 中画出了函数
中画出了函数![]() 的图象,如图所示.请在同一坐标系中画出函数
的图象,如图所示.请在同一坐标系中画出函数![]() 的图象;
的图象;
![]() 继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当
继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当![]() 为等腰三角形时,线段
为等腰三角形时,线段![]() 长度的近似值.(结果保留一位小数).
长度的近似值.(结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com