
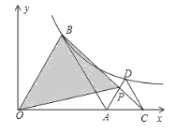
【题目】如图,△AOB和△ACD均为正三角形,且顶点B、D均在双曲线![]() (x>0)上,若图中S△OBP=4,则k的值为( )
(x>0)上,若图中S△OBP=4,则k的值为( )
A.![]() B.-
B.-![]() C.-4D.4
C.-4D.4
科目:初中数学 来源: 题型:
【题目】已知抛一枚质地均匀的硬币正面朝上的概率为![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.连续抛一枚均匀硬币2次必有1次正面朝上
B.连续抛一枚均匀硬币5次,正面都朝上是不可能事件
C.大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D.通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年1月份,某药店计划购进一批甲、乙两种型号的口罩,已知一袋甲种口罩的进价与一袋乙种口罩的进价和为40元,用90元购进甲种口罩的袋数与用150元购进乙种口罩的袋数相同.求每袋甲种、乙种口罩的进价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量![]() 与函数值
与函数值![]() 的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
| … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 6 | 3 | 2 | 1.5 | 1.2 | 1 | … |
(1)当![]() 时,
时,![]() ;
;
(2)根据表中数值描点![]() ,并画出函数图象;
,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .
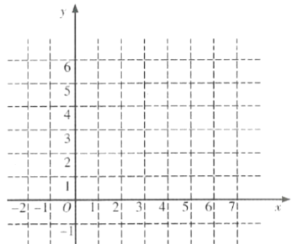
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,关于
中,关于![]() 的二次函数
的二次函数![]() 的图象过点
的图象过点![]() ,
,![]() .
.
(1)求这个二次函数的表达式;
(2)求当![]() 时,
时,![]() 的最大值与最小值的差;
的最大值与最小值的差;
(3)一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象交点的横坐标分别是
的图象交点的横坐标分别是![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
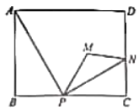
【题目】如图,在矩形ABCD中,已知![]() ,
,![]() ,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作
,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作![]() 的角平分线交边CD于点N.则线段MN的最小值为_______________
的角平分线交边CD于点N.则线段MN的最小值为_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017河北24题10分)如图,直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() ,
,![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
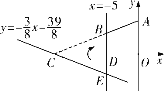
(1)求点![]() ,
,![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,而
的位置,而![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(﹣3,3),过点A的直线y=![]() x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
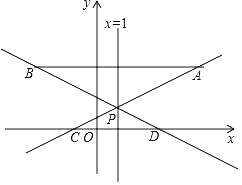
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的![]() 处飞出(
处飞出(![]() 在
在![]() 轴上),运动员乙在距
轴上),运动员乙在距![]() 点6米的
点6米的![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
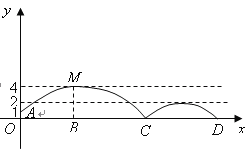
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点![]() 距守门员多少米?(取
距守门员多少米?(取![]() )
)
(3)运动员乙要抢到第二个落点![]() ,他应再向前跑多少米?
,他应再向前跑多少米?
(取![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com