
【题目】通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量![]() 与函数值
与函数值![]() 的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
| … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 6 | 3 | 2 | 1.5 | 1.2 | 1 | … |
(1)当![]() 时,
时,![]() ;
;
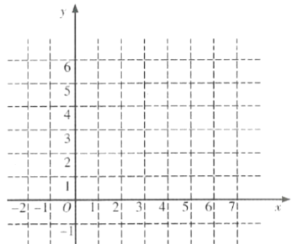
(2)根据表中数值描点![]() ,并画出函数图象;
,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() 连接
连接![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.
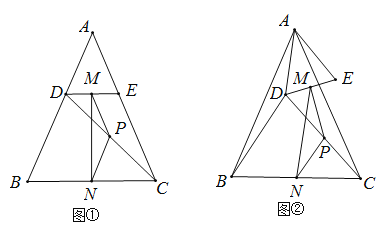
[观察猜想]图①,线段![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() _____
_____![]() ;
;
[探究证明]把![]() 绕点
绕点![]() 逆时针方向旋转到图②的位置,连结
逆时针方向旋转到图②的位置,连结![]() ,上述猜想的结论是否成立,请说明理由.
,上述猜想的结论是否成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第33个国际禁毒日到来之际,贵阳市策划了以“健康人生绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划采购甲、乙两种不同型号的平板电脑共20台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价为2500元,售价3000元.
(1)设该商店购进甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数表达式.
(2)若该商店采购两种平板电脑的总费用不超过39200元,全部售出所获利润不低于8500元,请设计出所有采购方案,并求出使商店获得最大利润的采购方案及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,动点
,动点![]() ,
,![]() 分别从
分别从![]() 点,
点,![]() 点同时以每秒1个单位长度的速度出发,且分别在边
点同时以每秒1个单位长度的速度出发,且分别在边![]() 上沿
上沿![]() ,
,![]() 的方向运动,当点
的方向运动,当点![]() 运动到点
运动到点![]() 时,
时,![]() 两点同时停止运动,设点
两点同时停止运动,设点![]() 运动的时间为
运动的时间为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
(1)如图2,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)在(1)的条件下,试探究线段![]() 三者之间的等量关系,并加以证明;
三者之间的等量关系,并加以证明;
(3)如图3,当![]() 时,延长
时,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
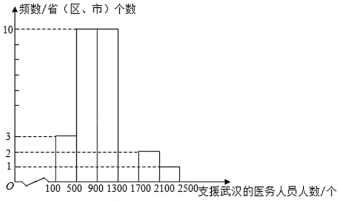
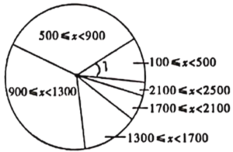
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
![]() 市派出的1614名医护人员中有404人是“90后”;
市派出的1614名医护人员中有404人是“90后”;
![]() 市派出的338名医护人员中有103人是“90后”;
市派出的338名医护人员中有103人是“90后”;
![]() 市某医院派出的148名医护人员中有83人是“90后”.
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
查看答案和解析>>
科目:初中数学 来源: 题型:
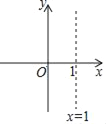
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在学习中遇到这样一个问题:
如图,点![]() 是弧
是弧![]() 上一动点,线段
上一动点,线段![]() 点
点![]() 是线段
是线段![]() 的中点,过点
的中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .当
.当![]() 为等腰三角形时,求线段
为等腰三角形时,求线段![]() 的长度.
的长度.

小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:
![]() 根据点
根据点![]() 在弧
在弧![]() 上的不同位置,画出相应的图形,测量线段
上的不同位置,画出相应的图形,测量线段![]() 的长度,得到下表的几组对应值.
的长度,得到下表的几组对应值.
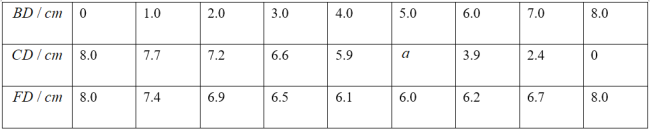
操作中发现:
①"当点![]() 为弧
为弧![]() 的中点时,
的中点时, ![]() ".则上中
".则上中![]() 的值是
的值是
②"线段![]() 的长度无需测量即可得到".请简要说明理由;
的长度无需测量即可得到".请简要说明理由;
![]() 将线段
将线段![]() 的长度作为自变量
的长度作为自变量![]() 和
和![]() 的长度都是
的长度都是![]() 的函数,分别记为
的函数,分别记为![]() 和
和![]() ,并在平面直角坐标系
,并在平面直角坐标系![]() 中画出了函数
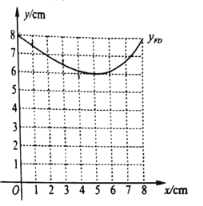
中画出了函数![]() 的图象,如图所示.请在同一坐标系中画出函数
的图象,如图所示.请在同一坐标系中画出函数![]() 的图象;
的图象;
![]() 继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当
继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当![]() 为等腰三角形时,线段
为等腰三角形时,线段![]() 长度的近似值.(结果保留一位小数).
长度的近似值.(结果保留一位小数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com