
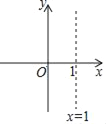
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
【答案】(1)-4(2)y=x2﹣2x+![]() 或y=x2﹣2x﹣8(3)当﹣3<c<0时,抛物线与x轴有且只有一个公共点
或y=x2﹣2x﹣8(3)当﹣3<c<0时,抛物线与x轴有且只有一个公共点
【解析】
(1)根据二次函数的性质,求出顶点的纵坐标即可解决问题;
(2)分两种情形①当点A、B都在原点的右侧时,如解图1,②当点A在原点的左侧,点B在原点的右侧时,如解图2,分别求解即可;
(3)把问题转化为不等式即可解决问题;
(1)当c=﹣3时,抛物线为y=x2﹣2x﹣3,
∴抛物线开口向上,有最小值,
∴y最小值=![]() =﹣4,
=﹣4,
∴y1的最小值为﹣4;
(2)抛物线与x轴有两个交点,
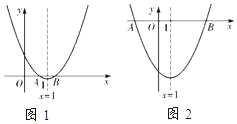
①当点A、B都在原点的右侧时,如解图1,
设A(m,0),
∵OA=![]() OB,
OB,
∴B(2m,0),
∵二次函数y=x2﹣2x+c的对称轴为x=1,
由抛物线的对称性得1﹣m=2m﹣1,解得m=![]() ,
,
∴A(![]() ,0),
,0),
∵点A在抛物线y=x2﹣2x+c上,
∴0=![]() ﹣
﹣![]() +c,解得c=
+c,解得c=![]() ,
,
此时抛物线的解析式为y=x2﹣2x+![]() ;
;
②当点A在原点的左侧,点B在原点的右侧时,如解图2,
设A(﹣n,0),
∵OA=![]() OB,且点A、B在原点的两侧,
OB,且点A、B在原点的两侧,
∴B(2n,0),
由抛物线的对称性得n+1=2n﹣1,
解得n=2,
∴A(﹣2,0),
∵点A在抛物线y=x2﹣2x+c上,
∴0=4+4+c,解得c=﹣8,
此时抛物线的解析式为y=x2﹣2x﹣8,
综上,抛物线的解析式为y=x2﹣2x+![]() 或y=x2﹣2x﹣8;
或y=x2﹣2x﹣8;
(3)∵抛物线y=x2﹣2x+c与x轴有公共点,
∴对于方程x2﹣2x+c=0,判别式b2﹣4ac=4﹣4c≥0,
∴c≤1.
当x=﹣1时,y=3+c;当x=0时,y=c,
∵抛物线的对称轴为x=1,且当﹣1<x<0时,抛物线与x轴有且只有一个公共点,
∴3+c>0且c<0,解得﹣3<c<0,
综上,当﹣3<c<0时,抛物线与x轴有且只有一个公共点.


科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量![]() 与函数值
与函数值![]() 的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
| … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 6 | 3 | 2 | 1.5 | 1.2 | 1 | … |
(1)当![]() 时,
时,![]() ;
;
(2)根据表中数值描点![]() ,并画出函数图象;
,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
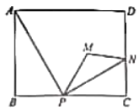
【题目】如图,在矩形ABCD中,已知![]() ,
,![]() ,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作
,点P是边BC上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接MP,作![]() 的角平分线交边CD于点N.则线段MN的最小值为_______________
的角平分线交边CD于点N.则线段MN的最小值为_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
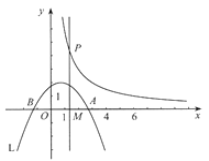
【题目】(2017河北24题10分)如图,直角坐标系![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴及直线
轴及直线![]() 分别交于点
分别交于点![]() ,
,![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() .
.
(1)求点![]() ,
,![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(2)设面积的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 时,嘉琪有个想法:“将
时,嘉琪有个想法:“将![]() 沿
沿![]() 轴翻折到
轴翻折到![]() 的位置,而
的位置,而![]() 与四边形
与四边形![]() 拼接后可看成
拼接后可看成![]() ,这样求
,这样求![]() 便转化为直接求
便转化为直接求![]() 的面积不更快捷吗?”但大家经反复验算,发现
的面积不更快捷吗?”但大家经反复验算,发现![]() ,请通过计算解释他的想法错在哪里.
,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
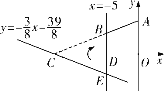
【题目】如图,抛物线L: ![]() (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线
(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线![]() 于点P,且OA·MP=12.
于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(5,3),点B(﹣3,3),过点A的直线y=![]() x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
x+m(m为常数)与直线x=1交于点P,与x轴交于点C,直线BP与x轴交于点D.
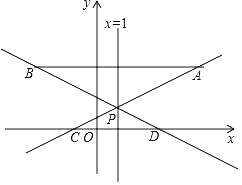
(1)求点P的坐标;
(2)求直线BP的解析式,并直接写出△PCD与△PAB的面积比;
(3)若反比例函数![]() (k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
(k为常数且k≠0)的图象与线段BD有公共点时,请直接写出k的最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据衢州市统计局发布的统计数据显示,衢州市近5年国民生产总值数据如图1所示,2016年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示。
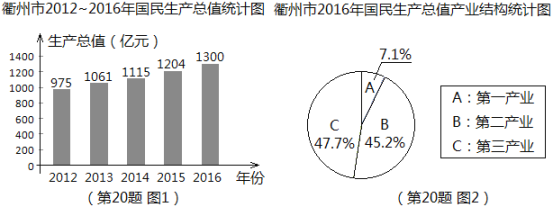
请根据图中信息,解答下列问题:
(1)求2016年第一产业生产总值(精确到1亿元);
(2)2016年比2015年的国民生产总值增加了百分之几(精确到1%)?
(3)若要使2018年的国民生产总值达到1573亿元,求2016年至2018年我市国民生产总值平均年增长率(精确到1%)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com