
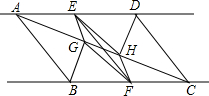
 如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分.
如图,已知直线m∥n,A,D两点在直线m上,B,C两点在直线n上,且AB∥CD,E,F分别是AD,BC的中点,BG⊥AC,DH⊥AC,点G,H分别是垂足.求证:EF与GH互相平分. 分析 由直线m∥n,A,D两点在直线m上,B,C两点在直线n上,得到AD∥BC,由于AB∥CD,推出四边形ABCD是平行四边形,根据平行四边形的性质得到AD=BC,推出AE=CF,根据BG⊥AC,DH⊥AC,得到∠AHD=∠CGB=90°,根据直角三角形的性质得到EH=GF,证得△ADH≌△CBG,得到AH=CG,作出AG=CH,然后由△AEG≌△CFH,得到EG=FH,证得四边形EGFH是平行四边形,即可得到结论.
解答 证明:∵直线m∥n,A,D两点在直线m上,B,C两点在直线n上,
∴AD∥BC,
∴∠DAC=∠ACB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∴AD=BC,
∵E,F分别是AD,BC的中点,
∴AE=CF,
∵BG⊥AC,DH⊥AC,
∴∠AHD=∠CGB=90°,
∴HE=$\frac{1}{2}$AD,GF=$\frac{1}{2}$BC,
∴EH=GF,
在△ADH与△CBG中,$\left\{\begin{array}{l}{∠DAH=∠BCG}\\{∠AHD=∠CGB}\\{AD=BC}\end{array}\right.$,
∴AH=CG,
∴AG=CH,
在△AEG与△CFH中,$\left\{\begin{array}{l}{AE=CF}\\{∠EAG=∠FCH}\\{AG=CH}\end{array}\right.$,
∴△AEG≌△CFH,
∴EG=FH,
∴四边形EGFH是平行四边形,
∴EF与GH互相平分.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,直角三角形的性质,熟练掌握这些定理是解题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
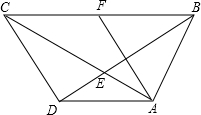 如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD相交于点E,∠ADB=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
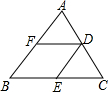 如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.
如图,△ABC中,D是AC的中点,DF∥BC,交AB于F,DE∥AB,交BC于E,试判断:AF与DE,CE与DF的长度之间有什么关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
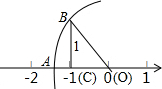 如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )
如图,直角三角形OBC中,BC=1,OC在数轴上,且点O、C对应的实数分别是0,-1,以点O为圆心,OB的长为半径画弧,与数轴的负半轴交于点A,设点A所对应的实数为x,则x2-10的立方根为( )| A. | $\sqrt{2}$-10 | B. | -$\sqrt{2}$-10 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
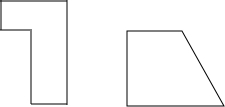 某公园准备用如图所示的材料给一块矩形的场地铺地面
某公园准备用如图所示的材料给一块矩形的场地铺地面查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
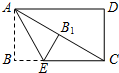 如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com