练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知A（1，6）B（n，﹣2）是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点，直线与y轴交于C点．
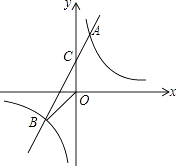
    （1）求反比例函数和一次函数的表达式；
    （2）求△BOC的面积；
    （3）直接写出不等式kx+b﹣ ＞0的解集．

    【答案】
    （1）解：∵A（1，6）在反比例函数y= 的图象上，

    ∴m=6，

    ∴反比例函数的解析式为：y=

    ∵B（n，﹣2）在反比例函数y= 的图象上，

    ∴n=﹣3，

    ∵A（1，6），B（n，﹣2）是一次函数y=kx+b上的点，

    ∴

    解得： ，

    ∴一次函数的解析式：y=2x+4，


    （2）解：令x=0代入y=2x+4，

    ∴y=4，

    ∴C（0，4），

    ∴OC=4，

    ∴S△BOC= ×4×3=6，


    （3）解：由图象可知：﹣3＜x＜0或x＞1
    【解析】（1）将A的坐标代入反比例函数的解析式即可求出m的值，然后将B的坐标代入反比例函数解析式即可求出n的值．最后将A、B的坐标代入一次函数的解析式即可求出一次函数的解析式．（2）求出点C的坐标，然后根据三角形面积公式即可求出△BOC的面积．（3）即找出一次函数的图象位于反比例函数的图象上方时x的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．

    (1)求证：∠A+∠C＝∠B+D；

    (2)如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD、AB分别相交于点M、N．

    ①以线段AC为边的“8字型”有　 　个，以点O为交点的“8字型”有　 　个；

    ②若∠B＝100°，∠C＝120°，求∠P的度数；

    ③若角平分线中角的关系改为“∠CAP＝∠CAB，∠CDP＝∠CDB”，试探究∠P与∠B、∠C之间存在的数量关系，并证明理由．

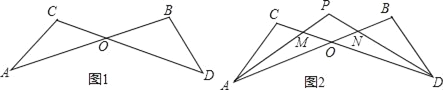
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，D在边AC上，且．

    如图1，填空______，______

    如图2，若M为线段AC上的点，过M作直线于H，分别交直线AB、BC与点N、E．

    求证：是等腰三角形；

    试写出线段AN、CE、CD之间的数量关系，并加以证明．

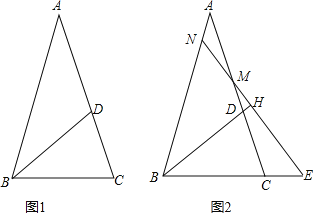
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】任何一个正整数n都可以进行这样的分解：n＝p×q（p、q是正整数，且p≤q）．如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并且规定F（n）＝．例如18＝1×18＝2×9＝3×6，这时就有F（18）＝．请解答下列问题：

    (1)计算：F（24）；

    (2)当n为正整数时，求证：F（n3+2n2+n）＝．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，BO平分∠ABC，CO平分∠ACB，MN经过点O，与AB，AC相交于点M，N，且MN∥BC，若AB=5，AC=6，则△AMN的周长为（ ）

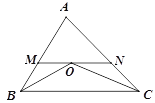
    A. 7 B. 9 C. 11 D. 16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A(a，0)，B(b，0)，且+| b-6|=0.

    （1）求A，B的坐标；

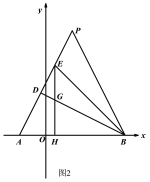
    （2）如图2，点P为AB的垂直平分线上一点，BD⊥AP于点D，BE是△PBD的角平分线，EH⊥AB于点H，交BD于点G，若AD=m，DE=n，求△BEG的面积（用含m，n的式子表示）；

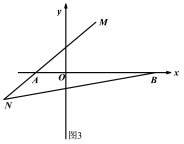
    （3）如图3，点M在AB的垂直平分线上，且∠MAB=40°，点N在MA的延长线上，且MN=8，求∠ABN的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），已知抛物线y=ax2+bx﹣3的对称轴为x=1，与x轴分别交于A、B两点，与y轴交于点C，一次函数y=x+1经过A，且与y轴交于点D．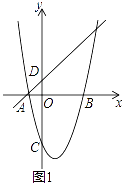

    （1）求该抛物线的解析式．
    （2）如图（2），点P为抛物线B、C两点间部分上的任意一点（不含B，C两点），设点P的横坐标为t，设四边形DCPB的面积为S，求出S与t的函数关系式，并确定t为何值时，S取最大值？最大值是多少？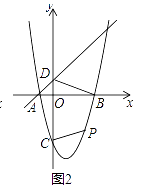

    （3）如图（3），将△ODB沿直线y=x+1平移得到△O′D′B′，设O′B′与抛物线交于点E，连接ED′，若ED′恰好将△O′D′B′的面积分为1：2两部分，请直接写出此时平移的距离．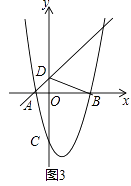

    查看答案和解析>>

    科目：初中数学 来源： 题型：

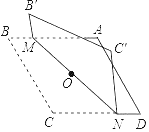
    【题目】对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O折叠菱形，使B，B′两点重合，MN是折痕．若B'M=1，则CN的长为____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

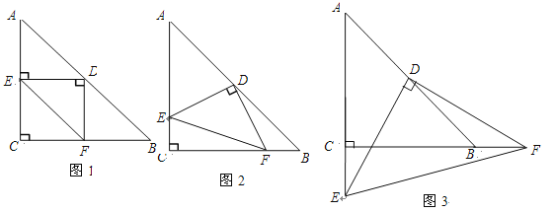
    【题目】 已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．当∠EDF绕D点旋转到DE⊥AC于E时（如图1），易证．当∠EDF绕D点旋转到DE和AC不垂直时，在图2和图3这两种情况下，上述结论是否成立? 若成立，请给予证明；若不成立，，，又有怎样的数量关系？请写出你的猜想，不需证明．

    查看答案和解析>>

    同步练习册答案