
【题目】如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
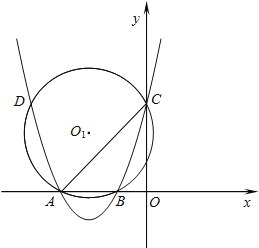
(1)求抛物线的解析式;
(2)求⊙O1的半径.
【答案】(1)y=x2+4x+3;(2)![]() .
.
【解析】
试题分析:(1)利用待定系数法求出抛物线的解析式;
(2)如图所示,由圆周角定理,确定△BO1C为等腰直角三角形,从而求出半径的长度.
解:(1)∵抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),
∴![]() ,
,
解得a=1,b=4,
∴抛物线的解析式为:y=x2+4x+3;
(2)由(1)知,抛物线解析式为:y=x2+4x+3,
∵令x=0,得y=3,
∴C(0,3),
∴OC=OA=3,则△AOC为等腰直角三角形,
∴∠CAB=45°,
在Rt△BOC中,由勾股定理得:BC=![]() =
=![]() ,
,
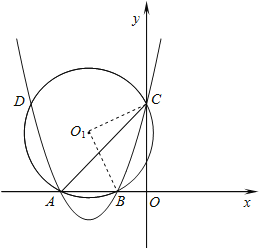
如图1所示,连接O1B、O1B,
由圆周角定理得:∠BO1C=2∠BAC=90°,
∴△BO1C为等腰直角三角形,
∴⊙O1的半径O1B=![]() BC=
BC=![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
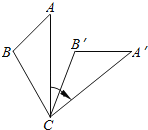
A.110° B.80° C.40° D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.若两弦相等,则它们所对的弧相等
B.若弦长等于半径,则弦所对的劣弧的度数为60°
C.若两弧不等,则大弧所对的圆心角较大
D.若两弧的度数相等,则两条弧是等弧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=![]() (x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )

A.![]() B.
B.![]() +2 C.2
+2 C.2![]() +1 D.
+1 D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com