
【题目】请根据图中信息回答下列问题:

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某人想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
 核心素养学练评系列答案
核心素养学练评系列答案科目:初中数学 来源: 题型:
【题目】如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘. 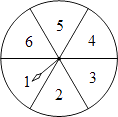
(1)自由转动转盘,当它停止转动时,指针指向的数大于4的概率为;
(2)请用画树状图法或列表法等方式求出“两次转动转盘,指针指向的数都大于4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF. 
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用白铁皮做罐头盒,每张铁皮可做盒身25个,或做盒底40个,一个盒身与两个盒底配成一套罐头盒.现有36张白铁皮,用多少张制盒身,多少张制盒底可以使盒身与盒底正好配套?
①设用x张制盒身,可得方程2×25x=40(36﹣x);
②设用x张制盒身,可得方程25x=2×40(36﹣x);
③设用x张制盒身,y张制盒底,可得方程组![]() ;
;
④设用x张制盒身,y张制盒底,可得方程组![]() ;其中正确的是( )
;其中正确的是( )
A. ①④ B. ②③ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员中进行射击比赛,两人在相同条件下各射击10次,射击的成绩如图所示.

根据图中信息,回答下列问题:
(1)甲的平均数是___________,乙的中位数是______________;
(2)分别计算甲、乙成绩的方差,并从计算结果来分析,你认为哪位运动员的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程指:含有一个未知数,且未知数的最高次数为2的等式,求一元二次方程![]() 解的方法如下:第一步:先将等式左边关于x的项进行配方,
解的方法如下:第一步:先将等式左边关于x的项进行配方, ![]() ,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,
,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,![]() ;第三步:根据平方的逆运算,求出
;第三步:根据平方的逆运算,求出![]() 或-3;第四步:求出
或-3;第四步:求出![]() .类比上述求一元二次方程根的方法,(1)解一元二次方程:
.类比上述求一元二次方程根的方法,(1)解一元二次方程:![]() ;
;
(2)求代数式![]() 的最小值;
的最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com