
如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为 .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E= ,求DE的长.
,求DE的长.

(1)CB=2,AP =2;
(2)证明见解析;
(3)DE=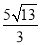 .
.
【解析】
试题分析:(1)根据圆周角定理由AC为直径得∠ABC=90°,在Rt△ABC中,根据勾股定理可计算出BC=2,再根据垂径定理由直径FG⊥AB得到AP=BP=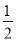 AB=2;
AB=2;
(2)易得OP为△ABC的中位线,则OP=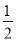 BC=1,再计算出
BC=1,再计算出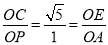 ,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;
(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E=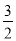 ,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=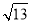 ,然后根据平行线分线段成比例定理得
,然后根据平行线分线段成比例定理得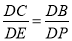 ,再利用比例性质可计算出DE=
,再利用比例性质可计算出DE=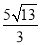 .
.
试题解析:(1)∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2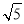 ,AB=4,
,AB=4,
∴BC=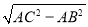 =2,
=2,
∵直径FG⊥AB,
∴AP=BP=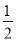 AB=2;
AB=2;
(2)∵AP=BP,
∴OP为△ABC的中位线,
∴OP=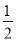 BC=1,
BC=1,
∴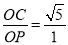 ,
,
而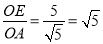 ,
,
∴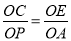 ,
,
∵∠EOC=∠AOP,
∴△EOC∽△AOP,
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(3)∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=
在Rt△BCD中,BC=2,tan∠DCB=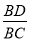 =
=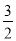 ,
,
∴BD=3,
∴CD=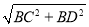 =
=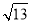 ,
,
∵BC∥EP,
∴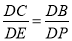 ,即
,即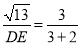 ,
,
∴DE=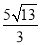 .
.
考点:切线的判定.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:填空题
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=A D.连接DE交对角线AC于H,连接BH.下列结论正确的是 .(填番号)
①AC⊥DE;② ;③CD=2DH;④
;③CD=2DH;④  .
.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:选择题
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是( )

A. B.
B. C.2
C.2 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:解答题
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川南充卷)数学(解析版) 题型:选择题
下列运算正确的是( )
A.a3a2=a5 B.(a2) 3=a5 C.a3+a3=a6 D.(a+b)2=a2+b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com