
���� ��1�����ݵ��ɵij��ȵ���ԭ����ȥ���̵ij��ȣ���ʽ���ɣ�
��2�����ݳ�����������ʽ�г�����ʽ��
��� �⣺��1��y=10-$\frac{1}{2}$x��x��10��������x���Ա�����y���Ա����ĺ�����
��2��V=30a2��a��0��������a���Ա�����V���Ա����ĺ�����
���� ���⿼�������һ�κ������ʵ�����⣬��֪�Ա�������ֵ����֪����ֵ���Ա�����ֵ���ǻ����⣬������Ŀ��Ϣ�ǽ���Ĺؼ���


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���䣨�꣩ | 18 | 19 | 20 | 21 |
| ���� | 5 | 4 | 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
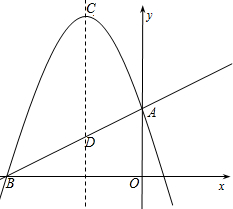 ��ͼ����ֱ֪��y=$\frac{1}{2}$x+$\frac{7}{2}$��x�ᡢy��ֱ��ཻ��B��A���㣬������y=ax2+bx+c����A��B���㣬�ҶԳ���Ϊֱ��x=-3��
��ͼ����ֱ֪��y=$\frac{1}{2}$x+$\frac{7}{2}$��x�ᡢy��ֱ��ཻ��B��A���㣬������y=ax2+bx+c����A��B���㣬�ҶԳ���Ϊֱ��x=-3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com