
 已知直角坐标系中,有等腰△ABC,其中两个顶点的坐标分别为A(1,0),B(4,4),第三个顶点C在坐标轴上,试画出C点的不同位置,并求出C点的坐标.
已知直角坐标系中,有等腰△ABC,其中两个顶点的坐标分别为A(1,0),B(4,4),第三个顶点C在坐标轴上,试画出C点的不同位置,并求出C点的坐标. 分析 由A(1,0),B(4,4),得到AB=$\sqrt{(4-1)^{2}+{4}^{2}}$=5,①当AB为腰时,以A为圆心AB的长为半径画圆,交坐标轴于E,H,J得到AE=AH=AJ=AB=5,根据勾股定理得到OH=$\sqrt{A{H}^{2}+O{A}^{2}}$=2$\sqrt{6}$,以B为圆心AB的长为半径画圆交坐标轴于A,F,G,I,于是得到BF=BG=BI=AB=5,设I(0,y),由两点间的距离公式求得y=1,得到I(0,1),F(7,0),G(0,7),②当AB为底时,AB的垂直平分线交x轴于D,交y轴于C,设C(0,n),D(m,0),于是得到CA=CB,AD=BD,根据两点间的距离公式求得C(0,$\frac{31}{8}$),D($\frac{31}{6}$,0),于是结论即可求出.
解答 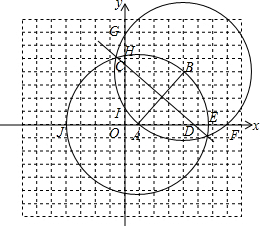 解:∵A(1,0),B(4,4),
解:∵A(1,0),B(4,4),
∴AB=$\sqrt{(4-1)^{2}+{4}^{2}}$=5,
①当AB为腰时,
以A为圆心AB的长为半径画圆,交坐标轴于E,H,J
∴AE=AH=AJ=AB=5,
∴OH=$\sqrt{A{H}^{2}+O{A}^{2}}$=2$\sqrt{6}$,
∴E(6,0),H(0,2$\sqrt{6}$),J(-4,0),
以B为圆心AB的长为半径画圆交坐标轴于A,F,G,I,
∴BF=BG=BI=AB=5,设I(0,y),∴(4-y)2+42=52,∴y=1,
∴I(0,1),F(7,0),G(0,7),
②当AB为底时,AB的垂直平分线交x轴于D,交y轴于C,
设C(0,n),D(m,0),
∴CA=CB,AD=BD,
∴12+n2=42+(4-n)2,(m-1)2=42+(m-4)2,
∴n=$\frac{31}{8}$,m=$\frac{31}{6}$,∴C(0,$\frac{31}{8}$),D($\frac{31}{6}$,0),
综上所述:符合条件的点有8个,分别为:C,D,E,F,G,H,I,J,
坐标为:C(0,$\frac{31}{8}$),D($\frac{31}{6}$,0),E(6,0),H(0,2$\sqrt{6}$),J(-4,0),I(0,1),F(7,0),G(0,7).
点评 本题考查了等腰三角形的性质,坐标与图形的性质,线段的垂直平分线的性质,特别是分类讨论思想的应用,不要漏解.


科目:初中数学 来源: 题型:解答题
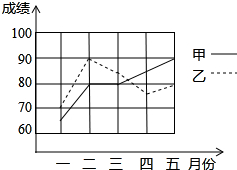 为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数)
为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,6 | B. | 12,16 | C. | 16,20 | D. | 20,24 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | $\frac{24}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com