
����Ŀ��(1)���21��20��2( )�� 22��21��2( ) ��23 ��22��2( )
(2)������ĸ��ʾ��n����ʽ������֤��ķ��֣�
(3)����(2)����ķ��֣���20��21��22��23������22016��22017��ֵ��
���𰸡���1��0��1��2����2��֤������������3��![]()
�������������������1������0���ݵ�����ͳ˷���������м��㼴����
��2���۲����ʽ�õ�2�����������Ǹ������ݵIJ�������н�С��2�ķǸ������ݣ���2n-2n-1=2n-1��nΪ����������
��3������21-20=20��22-21=21��23-22=22����22018-22017=22017��Ȼ��ѵ�ʽ����������ӣ��ұ����ұ���Ӽ�����⣮
�����������1��21-20=1=20��22-21=2=21��23-22=4=22��
�ʴ�Ϊ��0��1��2��
��2���۲�ɵã�2n-2n-1=2n-1��nΪ����������֤�����£�
2n-2n-1=2��2n-1-2n-1=2n-1��(2-1)=2n-1��
��3����21-20=20��
22-21=21��
23-22=22��
��
22018-22017=22017��
��22018-20=20+21+22+23+��+22016+22017��
��20+21+22+23+��+22016+22017��ֵΪ22018-1��
�����͡������
��������
27
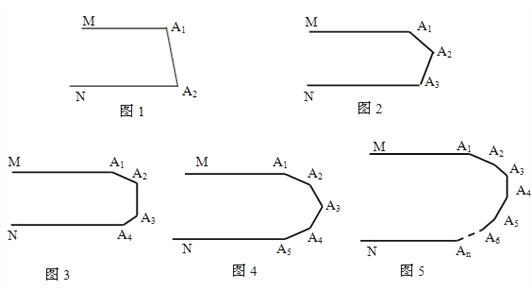
����Ŀ��(1) ��ͼ1��MA1��NA2�����A1+��A2=_________�ȣ�
��ͼ2��MA1��NA3�����A1+��A2+��A3=_________ �ȣ�
��ͼ3��MA1��NA4�����A1+��A2+��A3+��A4=_________�ȣ�
��ͼ4��MA1��NA5�����A1+��A2+��A3+��A4+��A5=_________�ȣ�
��ͼ5��MA1��NAn�����A1+��A2+��A3+��+��An=_________ �ȣ�
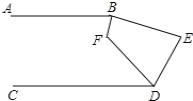
(2) ��ͼ,��֪AB��CD,��ABE����CDE��ƽ�����ཻ��F,��E=80��������BFD�Ķ���.
���𰸡���1�� 180�� 360�� 540��720��180��n-1������2��140��.
�������������������1�����ȹ�������MA 1 ��ƽ���ߣ���MA 1 ��NA 2 ���ɵø���ƽ�У�������ֱ��ƽ�У�ͬ���ڽǻ�����������ô���
��2������1���еĹ��ɿɵ���ABE+��E+��CDE=360�㣬���ԡ�ABE+��CDE=360��-80��=280�㣬����ΪBF��DFƽ�֡�ABE�͡�CDE�����ԡ�FBE+��FDE=140�㣬����Ϊ�ı��ε��ڽǺ�Ϊ360�㣬�����ɵô𰸣�
�����������1����ͼ1��
��MA 1 ��NA 2 ��
���A 1 +��A 2 =180�㣮
��ͼ2������A 2 ��A 2 C 1 ��A 1 M��
��MA 1 ��NA 3 ��
��A 2 C 1 ��A 1 M��NA 3 ��
���A 1 +��A 1 A 2 C 1 =180�㣬��C 1 A 2 A 3 +��A 3 =180�㣬
���A 1 +��A 2 +��A 3 =360�㣮
��ͼ3������A 2 ��A 2 C 1 ��A 1 M������A 3 ��A 3 C 2 ��A 1 M��
��MA 1 ��NA 3 ��
��A 2 C 1 ��A 3 C 2 ��A 1 M��NA 3 ��
���A 1 +��A 1 A 2 C 1 =180�㣬��C 1 A 2 A 3 +��A 2 A 3 C 2 =180�㣬��C 2 A 3 A 4 +��A 4 =180�㣬
���A 1 +��A 2 +��A 3 +��A 4 =540�㣮
��ͼ4������A 2 ��A 2 C 1 ��A 1 M������A 3 ��A 3 C 2 ��A 1 M��
��MA 1 ��NA 3 ��
��A 2 C 1 ��A 3 C 2 ��A 1 M��NA 3 ��
���A 1 +��A 1 A 2 C 1 =180�㣬��C 1 A 2 A 3 +��A 2 A 3 C 2 =180�㣬��C 2 A 3 A 4 +��A 3 A 4 C 3 =180�㣬��C 3 A 4 A 5 +��A 5 =180�㣬
���A 1 +��A 2 +��A 3 +��A 4 +��A 5 =720�㣻
�������������㷢���˹��ɣ���ͼ5��MA 1 ��NA n �����A 1 +��A 2 +��A 3 +��+��A n =180��n-1���ȣ�
�ʴ�Ϊ��180��360��540��720��180��n-1����

��2���ɣ�1���ɵ���ABE+��E+��CDE=360�㣬
�ߡ�E=80�㣬
���ABE+��CDE=360��-80��=280�㣬
�֡�BF��DFƽ�֡�ABE�͡�CDE��
���FBE+��FDE=140�㣬
�ߡ�FBE+��E+��FDE+��BFD=360�㣬
���BFD=360��-80��-140��=140�㣮


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ǵȱ������Σ�
��1����ͼ����D��AB���ϣ���E��AC���ϣ�BD��CE��BE��CD���ڵ�F�����ж�BF��CF��������ϵ��������֤����
��2����D��AB���ϵ�һ�����㣬��E��AC���ϵ�һ�����㣬��BD��CE��BE��CD���ڵ�F������BFD�ǵ��������Σ����FBD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������У�����֤����ABD�ա�ACD���ǣ� ��

A. BD=DC ,AB=AC B. ��ADB=��ADC,��BAD=��CAD
C. ��B=��C, BD=DC D. ��B=��C ,��BAD=��CAD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C����ͼ�б���˵�B�Ķ�Ӧ��B�䣮
��1���ڸ�������ֽ�л���ƽ�ƺ����A��B��C�䣻
�������������ǰ廭ͼ����㣺
��2������AB���ϵ�����CD��
��3������BC���ϵĸ���AE��
��4����A��B��C�������Ϊ______��

���𰸡���1����ͼ����������2����ͼ����������3����ͼ����������4��8.
����������:(1)��ͼ��ʾ: ![]() ��Ϊ����;
������;
(2)��ͼ��ʾ:CD�������������;
(3)��ͼ��ʾ:AE��ΪBC���ϵĸ�;
(4)![]() .
.
��![]() �����Ϊ8.
�����Ϊ8.
��ˣ�������ȷ����:8.
�����͡������
��������
24
����Ŀ����ͼ���SABC�У���A=40������ACB=104����BDΪAC���ϵĸߣ�BE�ǨSABC�Ľ�ƽ���ߣ����EBD�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֲ��ݮ���Ż�����22�ֲ�ݮ�ȴ�����������������������һ������ʡ��ֱ���������������������ڱ����г��������ܿ�����Ӱ�����Ż�ÿ��ֻ�ܲ���һ���������������Ҳ�ݮ������10�����۳�����10�죩���������������������������ÿ��������ÿ������������ұ���
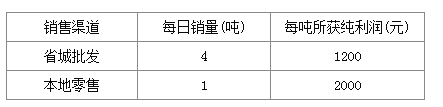
��1����һ���ֲ�ݮ����ʡ���������������������ڱ����г���������д������22�ֲ�ݮ��������y��Ԫ��������ʡ��ֱ�����������̵IJ�ݮ��x���֣�֮��ĺ�����ϵʽ��
��2������������22�ֲ�ݮ��������������ʹ�Ż������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������ʡ�еIJ��ֵ����������غ�����Ϊ������Լ��ˮ��ij������ˮ��˾��ȡ�ֶ��շѱ�����ͼ��ӳ����ÿ����ȡˮ��y��Ԫ������ˮ��x������֮��ĺ�����ϵ��
��1��С�������·���ˮ8����Ӧ��ˮ��______ Ԫ��
��2���������ֶ��շѱ���С�����������·ݷֱ�ˮ��26Ԫ��18Ԫ�������·ݱ����·ݽ�Լ��ˮ���ٶ֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2��A�ͳ���1��B�ͳ���������һ�ο��˻�10��.��1��A�ͳ���2��B�ͳ���������һ�ο��˻�11��.ij������˾����31�ֻ���ƻ�ͬʱ����A�ͳ�a����B�ͳ�b��,һ�����꣬��ÿ���������ػ���.����������Ϣ����������⣺
��1��1��A�ͳ���1��B�ͳ���������һ�ηֱ���˻�����ٶ֣�
��2�������������˾��������
��3����A�ͳ�ÿ�������ÿ��100Ԫ��B�ͳ�ÿ�������ÿ��120Ԫ.��ѡ����ʡǮ�����������������ٵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����У��ڵ�һ���ĵ��ǣ� ��
A.��2��3��B.����2����3��C.����2��3��D.��2����3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com