
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
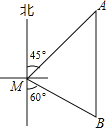
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
【答案】(1)90![]() 海里;(2)7.4小时.
海里;(2)7.4小时.
【解析】
(1)过点M作MD⊥AB于点D,根据AM=180海里以及△AMD的三角函数求出MD的长度;(2)根据三角函数求出MB的长度,然后计算.
解: (1)过点M作MD⊥AB于点D,
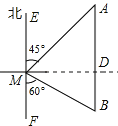
∵∠AME=45°,
∴∠AMD=∠MAD=45°,
∵AM=180海里,
∴MD=AMcos45°=90![]() (海里),
(海里),
答:渔船从A到B的航行过程中与小岛M之间的最小距离是90![]() 海里;
海里;
(2)在Rt△DMB中,
∵∠BMF=60°,
∴∠DMB=30°,
∵MD=90![]() 海里,
海里,
∴MB=60![]() 海里,
海里,
∴60![]() ÷20≈7.4(小时),
÷20≈7.4(小时),
答:渔船从B到达小岛M的航行时间约为7.4小时.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
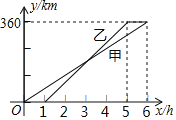
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲,y乙与x之间的函数图象如图所示.
(1)甲的速度是 km/h;
(2)当1≤x≤5时,求y乙关于x的函数关系式;
(3)当乙与A地相距240km时,直接写出甲与A地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
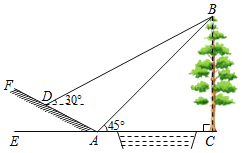
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(![]() ≈1.732,结果精确到0.1)
≈1.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
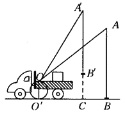
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至 A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊绳A′B′=AB.AB垂直地面 O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA![]() ,sinA′
,sinA′![]() .求此重物在水平方向移动的距离BC.
.求此重物在水平方向移动的距离BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,延长
的边长为4,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边在上方作正方形
为边在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
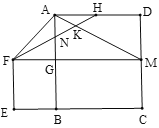
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为8,点
的边长为8,点![]() 是
是![]() 的内心,
的内心,![]() ,绕点
,绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①点
,给出下列四个结论:①点![]() 也一定是
也一定是![]() 的外心;②
的外心;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④
;④![]() 周长的最小值为6.上述结论中正确的个数是( )
周长的最小值为6.上述结论中正确的个数是( )
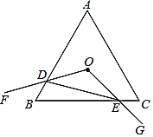
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由特殊到一般、类比、转化是数学学习和研究中经常用到的思想方法,下面是对一道几何题进行变式探究的思路,请你运用上述思想方法完成探究任务.
问题情境:在四边形![]() 中,
中,![]() 是对角线,
是对角线,![]() 为边
为边![]() 上一点,连接
上一点,连接![]() .以
.以![]() 为旋转中心,将线段
为旋转中心,将线段![]() 顺时针旋转,旋转角与
顺时针旋转,旋转角与![]() 相等,得到线段
相等,得到线段![]() ,连接
,连接![]() .
.
(1)特例如图1,若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 位置关系是_________.此时可以过点
位置关系是_________.此时可以过点![]() 作
作![]() 的平行线来对结论进行证明(这里不要求证明)
的平行线来对结论进行证明(这里不要求证明)
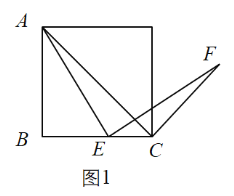
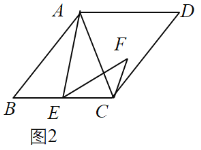
(2)拓展探究:如图2,若四边形![]() 是菱形,当
是菱形,当![]() 时,求
时,求![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴、y轴分别相交于A,B两点,与反比例函数
与x轴、y轴分别相交于A,B两点,与反比例函数![]() 在第二象限内交于点C,且点B是
在第二象限内交于点C,且点B是![]() 的中点.
的中点.
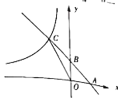
(1)求点C的坐标及k的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,﹣1).
(k≠0)的图象交于第二、四象限内的点A(a,4)和点B(8,﹣1).
(1)分别求出一次函数和反比例函数的解析式;
(2)延长AO与反比例函数交于点C,连接BC,求![]() ABC的面积.
ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com