
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
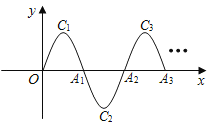
A.2B.﹣2C.﹣3D.3
科目:初中数学 来源: 题型:
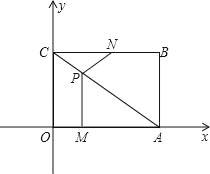
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了x秒.
(1)求P点的坐标(用含x的代数式表示);
(2)试求△NPC面积S的表达式,并求出面积S的最大值及相应的x值;
(3)设四边形OMPC的面积为S1,四边形ABNP的面积为S2,请你就x的取值范围讨论S1与S2的大小关系并说明理由;
(4)当x为何值时,△NPC是一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
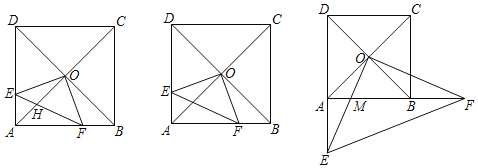
【题目】已知正方形ABCD,对角线AC、BD交于点O,线段OE⊥OF,且与边AD、AB交于点E、F.
(1)求证:OE=OF;
(2)连接EF,交AC于点H,若HF:AF=![]() :2,求OH:EF;
:2,求OH:EF;
(3)若E、F分别在DA、AB延长线上,OE与AB交于点M,若△MOF∽△EAF,AF=1,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个不透明的口袋中有4个形状、大小、材质完全相同的球,其中1个红色球,3个黄色球.
(1)从口袋中随机取出一个球(不放回),接着再取出一个球,请用树形图或列表的方法求取出的两个球一个是红色球,一个是黄色球的概率;
(2)小明往该口袋中又放入m个红色球和(m+2)个黄色球,再从口袋中随机取出一个球,这个球是黄色球的概率为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
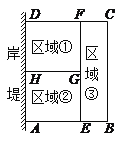
(1)求AE的长(用x的代数式表示)
(2)当y=108m2时,求x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
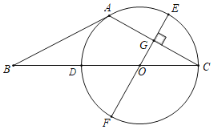
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,点O在BC上,⊙O经过点A,点C,且交BC于点D,直径EF⊥AC于点G.
(1)求证:AB是⊙O的切线;
(2)若AC=8,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
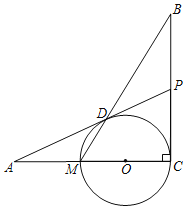
查看答案和解析>>
科目:初中数学 来源: 题型:
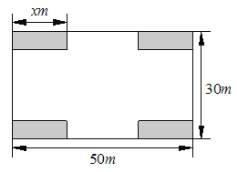
【题目】某小区业主委员会决定把一块长50![]() ,宽30
,宽30![]() 的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14
的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14![]() ,不大于26
,不大于26![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .
.
(1)直接写出:
①用![]() 的式子表示出口的宽度为_________;
的式子表示出口的宽度为_________;
②![]() 与
与![]() 的函数关系式及
的函数关系式及![]() 的取值范围__________________;
的取值范围__________________;
(2)若活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足;当x1<x2<0时(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B、C,且B在C的左侧,△ABC有一个内角为60°.则抛物线的解析式是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com