
【题目】某小区业主委员会决定把一块长50![]() ,宽30
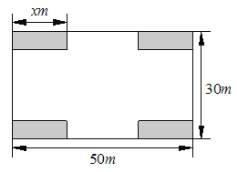
,宽30![]() 的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14
的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14![]() ,不大于26
,不大于26![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .
.
(1)直接写出:
①用![]() 的式子表示出口的宽度为_________;
的式子表示出口的宽度为_________;
②![]() 与
与![]() 的函数关系式及
的函数关系式及![]() 的取值范围__________________;
的取值范围__________________;
(2)若活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
【答案】(1)①50-2x;②y =-4x2+40x+1500(12≤x≤18)(2)69240元
【解析】
(1)①根据图形可得结论;
②根据题意可得y与x的关系式;
(2)根据列方程即可得到结论.
(1)①出口的宽度为:50-2x,
②绿化区的短边为:![]()
根据题意得,y=50×30-4x(x-10),
即y与x的函数关系式及x的取值范围为:y=-4x2+40x+1500(12≤x≤18);
故答案为:50-2x,y=-4x2+40x+1500(12≤x≤18);
(2)设费用为W,
由题意得,W=50(-4x2+40x+1500)+40×4x(x-10)=-40(x-5)2+76000,
∵a=-40<0,12≤x≤18
∴当x=18时,W最小,W最小值为69240元


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
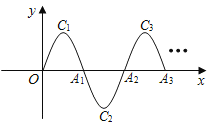
A.2B.﹣2C.﹣3D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店以每件80元的进价购进某种商品,原来按每件100元的售价出售,一天可售出50件;后经市场调查,发现这种商品每件的售价每降低2元,其销售量可增加10件.
(1)该网店销售该商品原来一天可获利润 元.
(2)设后来该商品每件售价降价![]() 元,网店一天可获利润
元,网店一天可获利润![]() 元.
元.
①若此网店为了尽可能增加该商品的销售量,且一天仍能获利1080元,则每件商品的售价应降价多少元?
②求![]() 与
与![]() 之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
查看答案和解析>>
科目:初中数学 来源: 题型:
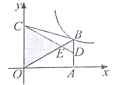
【题目】如图,四边形OABC中,AB∥OC,边OA在x轴的正半轴上,OC在y轴的正半轴上,点B在第一象限内,点D为AB的中点,CD与OB相交于点E,若△BDE、△OCE的面积分别为1和9,反比例函数y=![]() 的图象经过点B,则k=_______.
的图象经过点B,则k=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.
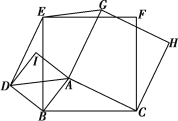
(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
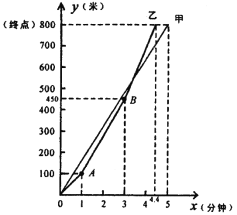
【题目】甲、乙两队在比赛时,路程y(米)与时间x(分钟)的函数图像如图所示,根据函数图像填空和解答问题:
(1)最先到达终点的是____________队,比另一队领先__________分钟到达.
(2)在比赛过程中,乙队在_____分钟和_____分钟时两次加速.
(3)假设乙队在第一次加速后,始终保持这个速度继续前进,那么甲、乙两队谁先到达终点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.
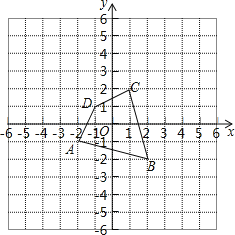
(1)画出旋转后的四边形A′B′C′D′;
(2)写出A′、B′、C′、D′的坐标;
(3)若每个小正方形的边长是1,请直接写出四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com