
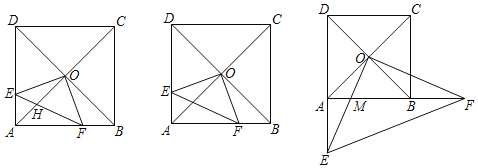
【题目】已知正方形ABCD,对角线AC、BD交于点O,线段OE⊥OF,且与边AD、AB交于点E、F.
(1)求证:OE=OF;
(2)连接EF,交AC于点H,若HF:AF=![]() :2,求OH:EF;
:2,求OH:EF;
(3)若E、F分别在DA、AB延长线上,OE与AB交于点M,若△MOF∽△EAF,AF=1,求正方形ABCD的边长.
【答案】(1)见解析;(2)![]() =
=![]() ;(3)正方形的边长为2﹣
;(3)正方形的边长为2﹣![]()
【解析】
(1)证明△EOA≌△FOB(ASA)即可解决问题;
(2)证明△OEH∽△FAH,推出![]() =
=![]() ,可得
,可得![]() =
=![]() =
=![]() ,由EF=
,由EF=![]() OE,可得
OE,可得![]() =
=![]() =
=![]() ,由此即可解决问题;
,由此即可解决问题;
(3)首先证明OA=OB=BF,设OA=OB=BF=x,则AB=![]() x,根据AF=1,构建方程即可解决问题.
x,根据AF=1,构建方程即可解决问题.
(1)证明:如图1中,
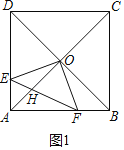
∵四边形ABCD是正方形,
∴OA=OB,AC⊥BD,∠EAO=∠OBF=45°,
∵OE⊥OF,
∴∠EFO=∠AOB=90°,
∴∠AOE=∠BOF,
∴△EOA≌△FOB(ASA),
∴OE=OF.
(2)解:如图1中,∵OE=OF,∠EOF=90°,
∴∠OEF=∠OFE=45°,
∵∠CAB=45°,
∴∠OEH=∠FAH,
∵∠EHO=∠AHF,
∴△OEH∽△FAH,
∴![]() FF0C
FF0C![]() ,
,
∵EF=![]() OE,
OE,
∴![]() ,
,
∴![]() =
=![]() ;
;
(3)解:如图2中,
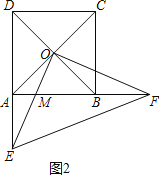
∵△MOF∽△EAF,
∴∠OFM=∠EAF,
由(1)可知△AOE≌△BOF,
∴OE=OF,
∵∠EOF=90°,
∴∠EFO=45°,
∴∠BFO=∠BFE=22.5°,
∵∠ABO=∠BFO+∠BOF=45°,
∴∠BOF=∠BOF=22.5°,
∴OB=BF,
∵OA=OB,
∴OA=OB=BF,设OA=OB=BF=x,则AB=![]() x,
x,
∵AF=AB+BF=![]() x+x=1,
x+x=1,
∴x=![]() ﹣1,
﹣1,
∴AB=AF﹣BF=1﹣(![]() ﹣1)=2﹣
﹣1)=2﹣![]() ,
,
∴正方形的边长为2﹣![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为S△ABC=36cm2,则梯形EDBC的面积SEDBC为( )

A.9B.18C.27D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,16,4分)如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点,那么△ADC′的面积是 .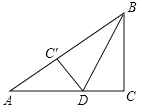
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )

A.50°B.60°
C.45°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
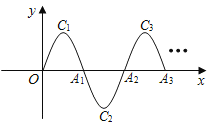
A.2B.﹣2C.﹣3D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.
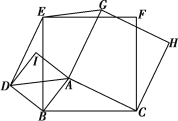
(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com