
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAO=AMAP.
(1)连接OP,证明:△ADM∽△APO;
(2)证明:PD是ΘO的切线;
(3)若AD=24,AM=MC,求![]() 的值.
的值.
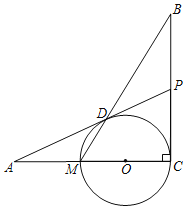
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明即可;
(2)通过证明OD⊥PA即可;
(3)连接CD,由(1)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,可得R2+242=9R2,推出R=6![]() ,推出OD=6
,推出OD=6![]() ,MC=12
,MC=12![]() ,由
,由![]() =
=![]() =
=![]() ,可得DP=12,再利用相似三角形的性质求出MD即可解决问题.
,可得DP=12,再利用相似三角形的性质求出MD即可解决问题.
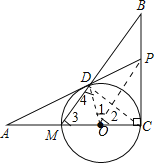
(1)证明:连接OD、OP、CD.
∵ADAO=AMAP,
∴![]() =
=![]() ,∠A=∠A,
,∠A=∠A,
∴△ADM∽△APO.
(2)∵△ADM∽△APO,
∴∠ADM=∠APO,
∴MD∥PO,
∴∠1=∠4,∠2=∠3,
∵OD=OM,
∴∠3=∠4,
∴∠1=∠2,
∵OP=OP,OD=OC,
∴△ODP≌△OCP,
∴∠ODP=∠OCP,
∵BC⊥AC,
∴∠OCP=90°,
∴OD⊥AP,
∴PD是⊙O的切线.
(3)连接CD.由(1)可知:PC=PD,
∵AM=MC,
∴AM=2MO=2R,
在Rt△AOD中,OD2+AD2=OA2,
∴R2+242=9R2,
∴R=6![]() ,
,
∴OD=6![]() ,MC=12
,MC=12![]() ,
,
∵![]() =
=![]() =
=![]() ,
,
∴DP=12,
∵O是MC的中点,
∴![]() =
=![]() =
=![]() ,
,
∴点P是BC的中点,
∴BP=CP=DP=12,
∵MC是⊙O的直径,
∴∠BDC=∠CDM=90°,
在Rt△BCM中,∵BC=2DP=24,MC=12![]() ,
,
∴BM=12![]() ,
,
∵△BCM∽△CDM,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴MD=4![]() ,
,
∴![]() =
=![]() =
=![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC≌△A′B′C,∠ACB=90°,∠B=50°,点B′在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )

A.50°B.60°
C.45°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
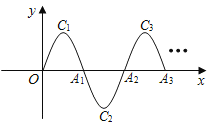
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
A.2B.﹣2C.﹣3D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
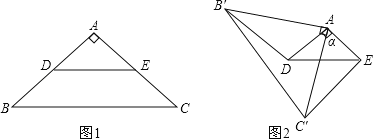
【题目】如图1,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转a角(0°<a<180°),得到△AB′C′(如图2),连接DB',EC'.
(1)探究DB'与EC'的数量关系,并结合图2给予证明;
(2)填空:
①当旋转角α的度数为_____时,则DB'∥AE;
②在旋转过程中,当点B',D,E在一条直线上,且AD=![]() 时,此时EC′的长为_____.
时,此时EC′的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店以每件80元的进价购进某种商品,原来按每件100元的售价出售,一天可售出50件;后经市场调查,发现这种商品每件的售价每降低2元,其销售量可增加10件.
(1)该网店销售该商品原来一天可获利润 元.
(2)设后来该商品每件售价降价![]() 元,网店一天可获利润
元,网店一天可获利润![]() 元.
元.
①若此网店为了尽可能增加该商品的销售量,且一天仍能获利1080元,则每件商品的售价应降价多少元?
②求![]() 与
与![]() 之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
之间的函数关系式,当该商品每件售价为多少元时,该网店一天所获利润最大?并求最大利润值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.
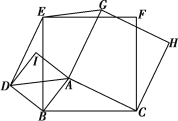
(1)求证:△BDE≌△BAC;
(2)求证:四边形ADEG是平行四边形.
(3)直接回答下面两个问题,不必证明:
①当△ABC满足条件_____________________时,四边形ADEG是矩形.
②当△ABC满足条件_____________________时,四边形ADEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,网格中每个小正方形的边长均为1,三个顶点的坐标分别为A(0,2),B(4,0),C(4,6).
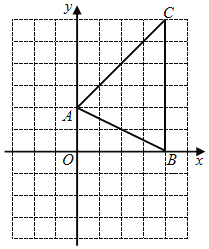
(1)画出△ABC向左平移2个单位长度得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为1:2,直接写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com