
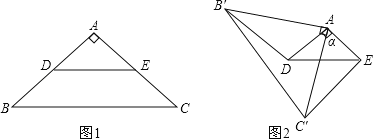
����Ŀ����ͼ1������ABC�У�AB��AC����BAC��90����D��E�ֱ���AB��AC�ߵ��е㣮����ABC�Ƶ�A˳ʱ����תa�ǣ�0����a��180�������õ���AB��C������ͼ2��������DB'��EC'��
��1��̽��DB'��EC'��������ϵ�������ͼ2����֤����
��2����գ�
�ٵ���ת�����Ķ���Ϊ_____ʱ����DB'��AE��
������ת�����У�����B'��D��E��һ��ֱ���ϣ���AD��![]() ʱ����ʱEC���ij�Ϊ_____��
ʱ����ʱEC���ij�Ϊ_____��
���𰸡���1��DB'��EC'��֤�������������2����60������![]() -1��
-1��
��������
��1������ת�����ʿɵá�DAE����B'AC'��90����AB'��AC'��������SAS����֤����ADB'�ա�AEC'���ɵ�DB'��EC'����2����ƽ���ߵ����ʺ�ֱ�������ε����ʿ���⣻��3����ȫ�������ε����ʿɵá�ADB'����AEC'��B'D��C'E���ɵ���ֱ�������ε����ʿɵ�B'C'��![]() AB'��4��DE��
AB'��4��DE��![]() AD��2���ɹ��ɶ�������EC'�ij���
AD��2���ɹ��ɶ�������EC'�ij���
��1��DB'��EC'��
�������£���AB��AC��D��E�ֱ���AB��AC�ߵ��е㣬
��AD��AE��
����ת�ɵã���DAE����B'AC'��90����AB'��AC'��
���DAB'����EAC'����AB'��AC'��AD��AE
���ADB'�ա�AEC'��SAS����
��DB����EC����
��2���١�DB����AE��
���B'DA����DAE��90����
��AD��![]() AB��AB=AB'��
AB��AB=AB'��
��AD��![]() AB'��
AB'��
���AB'D��30����
���DAB'��60����
����ת������60����
�ʴ�Ϊ60����
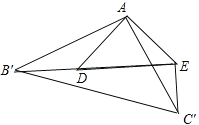
����ͼ������B'��D��E��һ��ֱ���ϣ�
��AD��![]() ��
��
��AB'��2![]() ��
��
�ߡ�ADE����AB'C'�ǵ���ֱ�������Σ�
��B'C'��![]() AB'��4��DE��
AB'��4��DE��![]() AD��2��
AD��2��
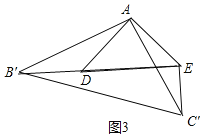
�ɣ�1����֪����ADB'�ա�AEC'��
���ADB'����AEC'��B'D��C'E��
�ߡ�ADB'����DAE+��AED����AEC'����AED+��DEC'��
���DEC'����DAE��90����
��B'C'2��B'E2+C'E2��
��16����2+EC'��2+C'E2��
��CE��![]() ��1��
��1��
�ʴ�Ϊ��![]() ��1��
��1��


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]()
(1)д������ͼ��Ŀ��ڷ���������ͶԳ���.
(2)�жϵ�![]() �Ƿ��ڸú���ͼ���ϣ���˵������.
�Ƿ��ڸú���ͼ���ϣ���˵������.
(3)����Ը�����������������Ľ���Ϊ����������ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
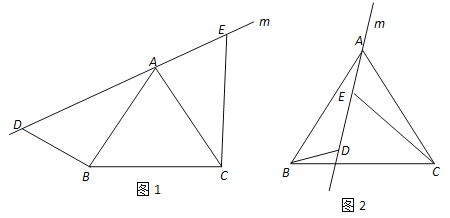
����Ŀ��̽����֤������1����ͼ1��ֱ��m������������ABC�Ķ���A����ֱ��m��ȡ���� D��E��ʹ�á�ADB=60������AEC=60����ͨ���۲������������߶�BD��CE��DE֮�������������ϵ��������֤����
��2������1���е�ֱ��m�Ƶ�A��ʱ�뷽����תһ���Ƕȵ���ͼ2��λ�ã���ʹ��ADB=120������AEC=120����ͨ���۲���������ֱ��д���߶�BD��CE��DE֮�������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ʡ���ϣ�ijˮ����ֳ������ˮ��İ��̣������㹻����Ϊһ�ߣ����ܳ�Ϊ80m��Χ����ˮ����Χ������ͼ��ʾ���٢ڢ���������������������������������ȣ���BC�ij���Ϊxm����������ABCD�����Ϊym2��
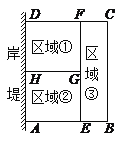
��1����AE�ij�����x�Ĵ���ʽ��ʾ��
��2����y=108m2ʱ����x��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
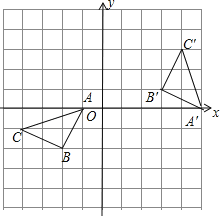
����Ŀ����ͼ��ʾ���������������У���ABC�Ķ�������ֱ�Ϊ����1��0��������2����2��������4����1������������ֱ������ϵ�а�Ҫ��ͼ�ͽ���������⣺
��1������ABC����ij�㰴˳ʱ�뷽����ת�õ���A��B'C'����ֱ��д����ת���ĵ��������ת�Ƕ�.
��2��������ABC���ڵ�A�����ĶԳƵġ�AED������ABC����һ��P��a��b������ֱ��д��������α任���P�ĶԳƵ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC��AC��Բ��O��AC�ϣ���M���C�ֱ���AC���O�Ľ��㣬��D��MB���O�Ľ��㣬��P��AD�ӳ�����BC�Ľ��㣬��ADAO��AMAP��
��1������OP��֤������ADM�ס�APO��
��2��֤����PD����O�����ߣ�
��3����AD��24��AM��MC����![]() ��ֵ��
��ֵ��
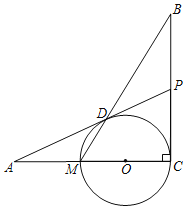
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
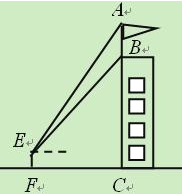
����Ŀ����ͼ��ij������BC����һ���AB��С������BC���12m��F������E��۲��˶���A������Ϊ52�����ײ�B������Ϊ45����С���Ĺ۲�������ľ���EFΪ.6m��
��������BC�ĸ߶ȣ�
�������AB�ĸ߶ȣ��������ȷ��0.1m���ο����ݣ�![]() ��1.41��sin52���0.79��tan52���1.28��
��1.41��sin52���0.79��tan52���1.28��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ�зֱ���к������������������������������������ĸ�С�����ֲ�֮ͬ�⣬С��û���κ�����ÿ������ǰ�Ƚ������������.
��1����������ȡһ�������������ϵĺ��ָպ����������ĸ��ʣ�
��2���״�����ȡһ�����Żأ��ٴ�����ȡһ��������״ͼ���б��������ȡ�����������ϵĺ���ǡ������������������������ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������һ���ߵ�ƽ�������������ߵij˻������dz�����������DZ��������Σ�
��1����֪��ABC�DZ��������Σ�AB��1��BC��2����AC�ij���
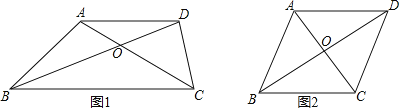
��2����ͼ1�����ı���ABCD�У�AB��AD���Խ���BDƽ�֡�ABC����BAC����ADC
����֤����ABC�DZ���������
����AB��DC����ͼ2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com