
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3 , 一等腰直角三角形ABC的三个顶点A,B,C分别在l1 , l2 , l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则 ![]() 的值为( )
的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣ ![]() x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.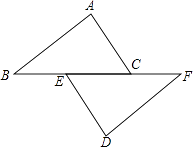
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年9月举行“全国中学生数学联赛”,成绩优异的选手可参加“全国中学生数学冬令营”,冬令营再选拔出50名优秀选手进入“国家集训队”.第31界冬令营已于2015年12月在江西省鹰谭一中成功举行.现将脱颖而出的50名选手分成两组进行竞赛,每组25人,成绩整理并绘制成如下的统计图:

请你根据以上提供的信息解答下列问题:
(1)请你将表格和条形统计图补充完整:
平均数 | 中位数 | 众数 | 方差 | |
一组 | 74 | __________ | __________ | 104 |
二组 | __________ | __________ | __________ | 72 |
(2)从本次统计数据来看,__________组比较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为(![]() ,
,![]() ),请解决以下问题:
),请解决以下问题:
(1)甲比乙晚出发几小时?
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过![]() h与乙相遇.
h与乙相遇.
①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com