
【题目】阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是
将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴ ![]() .方程
.方程![]() , 求
, 求![]() 、
、![]() .则有
.则有![]() ,
,
∴![]() .解得
.解得![]() .方程
.方程![]() ,则有
,则有![]() ,
,
∴![]() .解得
.解得![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
(1)若![]() .求
.求![]() 的值;
的值;
(2)![]() .求
.求![]() 的值;
的值;
(3)若![]() 表示△ABC的三边,且
表示△ABC的三边,且![]() ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
【答案】(1)a=﹣2;(2)﹣1;(3)△ABC为等边三角形.理由见解析.
【解析】
(1)运用完全平方公式将a2+4a+4=0变形为(a+2)2=0,即可求出a的值;
(2)首先将x2-4x+y2+6y+13=0分成两个完全平方式的形式,根据非负数的性质求出x、y的值,再代入(x+y)2017即可解答;
(3)先将已知等式利用配方法变形,再利用非负数的性质解题.
解:(1)∵a2+4a+4=0 ,∴(a+2)2=0 ,∴a+2=0,∴a1=a2=﹣2;
(2)∵x2﹣4x+y2+6y+13=0 , ∴(x﹣2)2+(y+3)2=0 ,∴x=2,y=﹣3,
∴(x+y)﹣2017=(2﹣3)﹣2017=﹣1;
(3)△ABC为等边三角形.理由如下:
∵a2+b2+c2﹣ac﹣ab﹣bc=0, ∴2a2+2b2+2c2﹣2ac﹣2ab﹣2bc=0
即a2+b2﹣2ab+b2+c2﹣2bc+a2+c2﹣2ac=0 ,∴(a﹣b)2+(b﹣c)2+(c﹣a)2=0
∴a﹣b=0,b﹣c=0,c﹣a=0 ,∴a=b=c,∴△ABC为等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,边长为2cm的等边△ABC的边BC在直线l上,两条距离为1cm的平行直线a和b垂直于直线l,直线a、b同时向右移动(直线a的起始位置在B点),运动速度为1cm/s,直到直线a到达C点时停止.在a、b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为S,求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
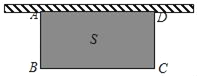
【题目】如图.利用一面墙(墙的长度不限),用20m的篱笆围成一个矩形场地ABCD.设矩形与墙垂直的一边AB=xm,矩形的面积为Sm2.
(1)用含x的式子表示S;
(2)若面积S=48m2,求AB的长;
(3)能围成S=60m2的矩形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
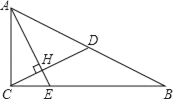
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
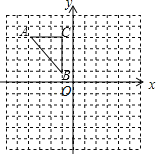
【题目】如图,△ABC在平面直角坐标系中,顶点的坐标分别为A(-4,4),B(-1,1),C(-1,4).
(1)画出与△ABC关于y轴对称的△A1B1C1.
(2)将△ABC绕点B逆时针旋转90°,得到△A2BC2,画两出△A2BC2.
(3)求线段AB在旋转过程中扫过的图形面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:

(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com