
【题目】一次函数![]() 与反比例函数
与反比例函数![]() 在同一直角坐标系内的图像的大致位置是图中的( )
在同一直角坐标系内的图像的大致位置是图中的( )
A. B.
B.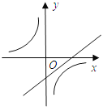 C.
C.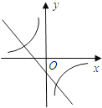 D.
D.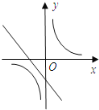
【答案】C
【解析】
分别根据反比例函数及一次函数图象的特点对四个选项进行逐一分析即可.
解:A、∵由反比例函数的图象在一、三象限可知,k>0,∴-k2-1<0,∴一次函数y=kx-k2-1的图象经过一、三、四象限,故本选项错误;
B、∵由反比例函数的图象在二、四象限可知,k<0,∴-k2-1<0,∴一次函数y=kx-k2-1的图象经过二、三、四象限,故本选项错误;
C、∵由反比例函数的图象在二、四象限可知,k<0,∴-k2-1<0,∴一次函数y=kx-k2-1的图象经过二、三、四象限,故本选项正确;
D、∵由反比例函数的图象在一、三象限可知,k>0,∴-k2-1<0,∴一次函数y=kx-k2-1的图象经过一、三、四象限,故本选项错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2 -16=0
(2)3x2+x-1=0
(3)3x(x-1)=2-2x
(4)9(3x-1)2 =(2-x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是
将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴ ![]() .方程
.方程![]() , 求
, 求![]() 、
、![]() .则有
.则有![]() ,
,
∴![]() .解得
.解得![]() .方程
.方程![]() ,则有
,则有![]() ,
,
∴![]() .解得
.解得![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
(1)若![]() .求
.求![]() 的值;
的值;
(2)![]() .求
.求![]() 的值;
的值;
(3)若![]() 表示△ABC的三边,且
表示△ABC的三边,且![]() ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB =xm,花园面积S.
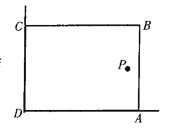
(1)求S关于x的函数关系式,求x的取值范围;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
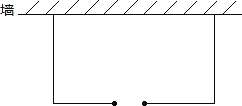
【题目】如图,要建一个底面积为130平方米的仓库,仓库一边靠墙(墙长16米),并在与墙平行的一边开道1米宽的门,现有能围成32米长的木板.请你设计如何搭建比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线:![]() 和直线:
和直线:![]() 交于点A(2,1);
交于点A(2,1);
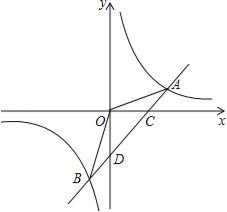
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象写出一次函数的值大于反比例函数的值的![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三位数,十位数字等于百位数字与个位数字的平均数,我们称这个三位数为“顺子数”,例如:630,123.
如果一个三位数,十位数字等于百位数字与个位数字的积的算术平方根,我们称这个三位数为“和谐数”,例如:139,124.
(1)若三位数![]() 是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
是“顺子数”,且各位数字之和大于7小于10,且百位数字a使得一元二次方程(a﹣5)x2+2ax+a﹣6=0有实数根,求这个“顺子数”;
(2)若三位数![]() 既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
既是“顺子数”又是“和谐数”,请探索a,b,c三者的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com