
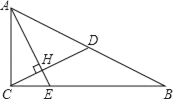
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】
试题(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:![]() ,即可得出sinB的值;
,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:![]() ,再由AB=
,再由AB=![]() ,得AC=2,则CE=1,从而得出BE.
,得AC=2,则CE=1,从而得出BE.
试题解析:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=![]() CH,
CH,
∴CH:AC=1:![]() ,
,
∴sinB=![]() ;
;
(2)∵sinB=![]() ,
,
∴AC:AB=1:![]() ,
,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB=![]() =
=![]() ,
,
设CE=x(x>0),则AE=![]() x,则
x,则![]() ,
,
∴CE=x=1,AC=2,
在Rt△ABC中,![]() ,
,
∵AB=2CD=![]() ,
,
∴BC=4,
∴BE=BC﹣CE=3.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向下平移3个单位,得到的抛物线过点( )
,将此抛物线向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)大致的图象如图,关于该二次函数,下列说法错误的是( )
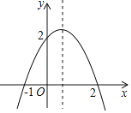
A. 函数有最大值
B. 对称轴是直线x=![]()
C. 当x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D. 当时﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D,E分别在边AB,AC上,将△ADE沿直线DE翻折,点A的对应点在边AB上,联结A′C,如果A′C=A′A,那么BD=___.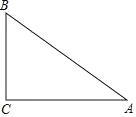
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(2x+3)2 -16=0
(2)3x2+x-1=0
(3)3x(x-1)=2-2x
(4)9(3x-1)2 =(2-x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是
将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程![]() ,则
,则![]() ,∴
,∴ ![]() .方程
.方程![]() , 求
, 求![]() 、
、![]() .则有
.则有![]() ,
,
∴![]() .解得
.解得![]() .方程
.方程![]() ,则有
,则有![]() ,
,
∴![]() .解得
.解得![]() ,根据以上材料解答下列各题:
,根据以上材料解答下列各题:
(1)若![]() .求
.求![]() 的值;
的值;
(2)![]() .求
.求![]() 的值;
的值;
(3)若![]() 表示△ABC的三边,且
表示△ABC的三边,且![]() ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
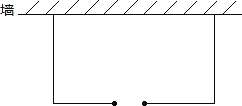
【题目】如图,要建一个底面积为130平方米的仓库,仓库一边靠墙(墙长16米),并在与墙平行的一边开道1米宽的门,现有能围成32米长的木板.请你设计如何搭建比较合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
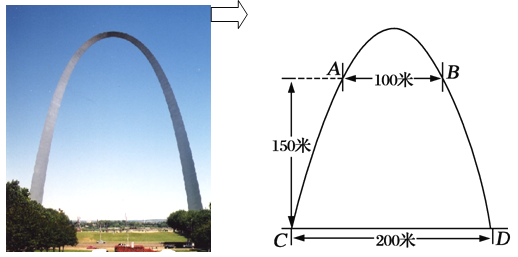
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com