
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).
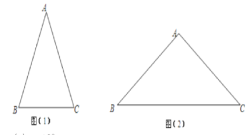
如图(1)在△![]() 中,
中,![]() ,底角
,底角![]() 的邻对记作
的邻对记作![]() ,这时
,这时![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义解下列问题:
(1)![]() = ;
= ;
(2)如图(2),在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的周长
的周长
【答案】(1)can30°=![]() ;(2)△ABC的周长=
;(2)△ABC的周长=![]() .
.
【解析】
(1)过点A作AD⊥BC于点D,根据∠B=30°,可得出BD=![]() AB,结合等腰三角形的性质可得出BC=
AB,结合等腰三角形的性质可得出BC=![]() AB,继而得出canB;
AB,继而得出canB;
(2)过点A作AE⊥BC于点E,根据canB=![]() ,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
,设BC=8x,AB=5x,再由S△ABC=24,可得出x的值,继而求出周长.
(1)(1)过点A作AD⊥BC于点D,
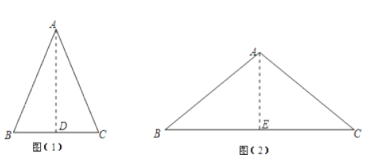
∵∠B=30°,
∴cos∠B=![]() =
=![]() ,
,
∴BD=![]() AB,
AB,
∵△ABC是等腰三角形,
∴BC=2BD=![]() AB,
AB,
故can30°=![]() =
=![]()
(2)∵在△ABC中, canB ![]() ,∴
,∴![]()
设![]()
过点A作AE![]() 垂足为点E,
垂足为点E,
∵AB=AC ∴![]()
∵![]() ∴
∴![]()
![]()
∴![]()
∴△ABC的周长=![]() .
.


科目:初中数学 来源: 题型:
【题目】解不等式组 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
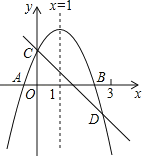
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).

(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2x+3.
(1)把函数关系式配成顶点式并求出图象的顶点坐标和对称轴.
(2)若图象与x轴交点为A.B,与y轴交点为C,求A、B、C三点的坐标;
(3)在图中画出图象.并求出△ABC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
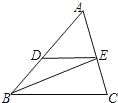
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果![]() =3,
=3,![]() =2,DE=6,求BC的长.
=2,DE=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
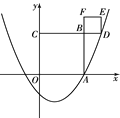
【题目】如图,抛物线![]() 与
与![]() 轴正半轴交于点A(3,0).以OA为边在
轴正半轴交于点A(3,0).以OA为边在![]() 轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则
轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF,则![]() = ,点E的坐标是 .
= ,点E的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为(1,2),(-2,3),(-1,0),把它们的横坐标和纵坐标都扩大到原来的2倍,得到点![]() ,
, ![]() ,
, ![]() .下列说法正确的是( )
.下列说法正确的是( )

A. △![]() 与△ABC是位似图形,位似中心是点(1,0)
与△ABC是位似图形,位似中心是点(1,0)
B. △![]() 与△ABC是位似图形,位似中心是点(0,0)
与△ABC是位似图形,位似中心是点(0,0)
C. △![]() 与△ABC是相似图形,但不是位似图形
与△ABC是相似图形,但不是位似图形
D. △![]() 与△ABC不是相似图形
与△ABC不是相似图形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com