
 如图,在△ABC中,AB=AC,BC=6,AF⊥BC于点F,BE⊥AC于点E,且点D是AB的中点,△DEF的周长是11,则AB=8.
如图,在△ABC中,AB=AC,BC=6,AF⊥BC于点F,BE⊥AC于点E,且点D是AB的中点,△DEF的周长是11,则AB=8.  课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | ∠A:∠B:∠C=l:2:3 | B. | 三边长为a,b,c的值为1,2,$\sqrt{3}$ | ||
| C. | 三边长为a,b,c的值为$\sqrt{11}$,2,4 | D. | a2=(c+b)(c-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
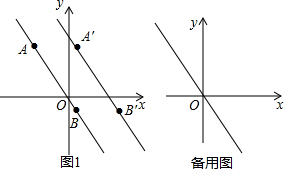 课本P152有段文字:把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x-3的图象.
课本P152有段文字:把函数y=2x的图象分别沿y轴向上或向下平移3个单位长度,就得到函数y=2x+3或y=2x-3的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数量/条 | 平均每条鱼的质量/kg | |
| 第1次捕捞 | 15 | 1.6 |
| 第2次捕捞 | 15 | 2.0 |
| 第3次捕捞 | 10 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 张大爷要围成一个矩形花圃,花圃的一边利用18米长的墙,另三边用总长为32米的篱笆恰好围成,围成的花圃是如图所示的矩形ABCD.
张大爷要围成一个矩形花圃,花圃的一边利用18米长的墙,另三边用总长为32米的篱笆恰好围成,围成的花圃是如图所示的矩形ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com