
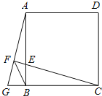
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,则
,则![]() 的长为________.
的长为________.
【答案】.![]()
【解析】
作FM⊥GC于M,则FM∥AB,由正方形的性质得出∠ABC=90°,AB=CB=6,由ASA证明△ABG≌△CBE,得出BG=BE,AG=CE,由AE=2BE,得出BG=BE=2,由勾股定理求出AGCE=AG=2![]() ,证明△AFE∽△CBE,得出对应边成比例求出AF=
,证明△AFE∽△CBE,得出对应边成比例求出AF=![]() ,求出FG=AGAF=
,求出FG=AGAF=![]() ,由平行线得出
,由平行线得出![]() ,求出FM=
,求出FM=![]() ,GM=
,GM=![]() ,得出BM=BGGM=
,得出BM=BGGM=![]() ,再由勾股定理求出BF即可.
,再由勾股定理求出BF即可.
作FM⊥GC于M,如图所示:

则FM∥AB,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=CB=6,
∴∠ABG=90°,
∴∠G+∠BAG=90°,
∵CF⊥AG,
∴∠AFE=∠CFG=90°,
∴∠G+∠BCE=90°,
∴∠BAG=∠BCE,
在△ABG和△CBE中,
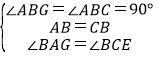 ,
,
∴△ABG≌△CBE(ASA),
∴BG=BE,AG=CE,
∵AE=2BE,
∴BE=2,AE=4,
∴BG=BE=2,∴CE=AG=![]() ,
,
∵∠AFE=∠ABC=90°,∠BAG=∠BCE,
∴△AFE∽△CBE,
∴![]() ,即
,即![]() ,
,
解得:AF=![]() ,
,
∴FG=AGAF=![]() ,
,
∵FM∥AB,
∴![]() ,
,
即![]() ,
,
解得:FM=![]() ,GM=
,GM=![]() ,
,
∴BM=BGGM=![]() ,
,
∴BF=![]() ;
;
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,以
,以![]() 为直径,
为直径,![]() 为圆心的半圆交
为圆心的半圆交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的角平分线,且
的角平分线,且![]() ,垂足为点
,垂足为点![]() .
.
![]() 判断直线
判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一学校为了解九年级学生某次体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
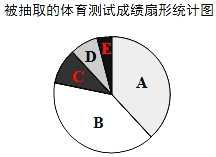
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有一个△DEF.
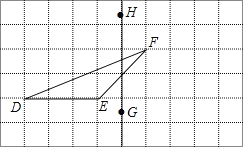
(1)画出△DEF关于直线HG的轴对称图形(不写画法);
(2)画EF边上的高(不写画法);
(3)若网格上的最小正方形边长为1,则△DEF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市南湖生态城某楼盘准备以每平方米![]() 元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米
元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米![]() 元的均价开盘销售.
元的均价开盘销售.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 王先生准备以开盘价均价购买一套
王先生准备以开盘价均价购买一套![]() 平方米的住房,开发商给予以下两种优惠方案:
平方米的住房,开发商给予以下两种优惠方案:
①打![]() 折销售;
折销售;
②不打折,一次性送装修费每平方米![]() 元,试问那种方案更优惠?
元,试问那种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校科技小组进行野外考察,途中遇到一片湿地,为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道,木板对地面的压强![]() 是木板面积
是木板面积![]() 的反比例函数,其图像如下图所示:
的反比例函数,其图像如下图所示:
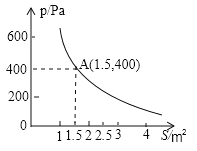
(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为![]() 时,压强是多少?
时,压强是多少?
(3)如果要求压强不超过![]() ,木板的面积至少要多大?
,木板的面积至少要多大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com