
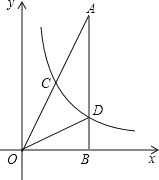
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
【答案】(1)反比例函数解析式为y=![]() ;
;
(2)C点坐标为(2,4)
【解析】
试题(1)由S△BOD=4可得BD的长,从而可得D的坐标,然后代入反比例函数解析式可求得K,从而得解析式为y=![]() ;
;
(2)由已知可确定A点坐标,再由待定系数法求出直线AB的解析式为y=2x,然后解方程组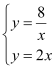 即可得到C点坐标.
即可得到C点坐标.
试题解析:(1)∵∠ABO=90°,OB=4,S△BOD=4,
∴![]() OB×BD=4,解得BD=2,
OB×BD=4,解得BD=2,
∴D(4,2)
将D(4,2)代入y=![]()
得2=![]()
∴k=8
∴反比例函数解析式为y=![]() ;
;
(2)∵∠ABO=90°,OB=4,AB=8,
∴A点坐标为(4,8),
设直线OA的解析式为y=kx,
把A(4,8)代入得4k=8,解得k=2,
∴直线AB的解析式为y=2x,
解方程组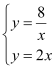 得
得![]() 或
或![]() ,
,
∴C点坐标为(2,4)


科目:初中数学 来源: 题型:
【题目】将正偶数按下表排成![]() 列:
列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
|
根据上表排列规律,则偶数![]() 应在第_________列.
应在第_________列.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
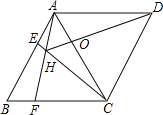
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
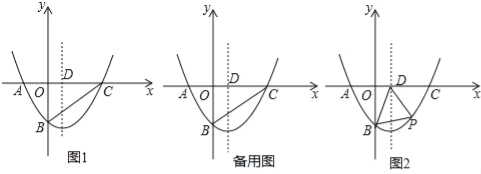
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为![]() 个单位长,且在圆周的三等分点处分别标上了数字
个单位长,且在圆周的三等分点处分别标上了数字![]() ,
,![]() ,
,![]() )上:先让原点与圆周上
)上:先让原点与圆周上![]() 所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上
所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点分别与圆周上
所对应的点分别与圆周上![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
所对应的点重合,这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.
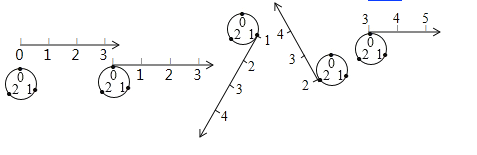
(1)圆周上数字![]() 与数轴上的数
与数轴上的数![]() 对应,则
对应,则![]() __________.
__________.
(2)数轴上的一个整数点刚刚绕过圆周![]() 圈(
圈(![]() 为正整数)后,并落在圆周上数字
为正整数)后,并落在圆周上数字![]() 所对应的位置,这个整数是____________.(用含
所对应的位置,这个整数是____________.(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=![]() 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=![]() 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某商场第一季度销售甲、乙两种冰箱若干台,其中乙种冰箱的数量比甲种冰箱多销售![]() 台,第二季度甲种冰箱的销量比第一季度增加
台,第二季度甲种冰箱的销量比第一季度增加![]() ,乙种冰箱的销量比第一季度增加
,乙种冰箱的销量比第一季度增加![]() ,且两种冰箱的总销量达到
,且两种冰箱的总销量达到![]() 台.
台.
求:(1)该商场第一季度销售甲种冰箱多少台?
(2)若每台甲种冰箱的利润为![]() 元,每台乙种冰箱的利润为
元,每台乙种冰箱的利润为![]() 元,则该商场第二季度销售冰箱的总利润是多少元?
元,则该商场第二季度销售冰箱的总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;……;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,……,则线段D1D2的长为______,线段Dn-1Dn的长为______(n为正整数).
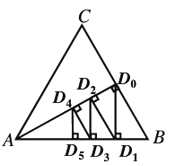
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com