
【题目】如图,直线![]() 和
和![]() 相交于点C,分别交x轴于点A和点B点P为射线BC上的一点。
相交于点C,分别交x轴于点A和点B点P为射线BC上的一点。
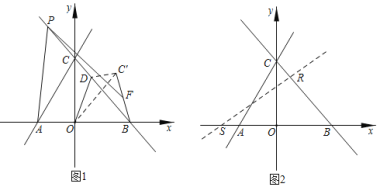
(1)如图1,点D是直线CB上一动点,连接OD,将![]() 沿OD翻折,点C的对应点为
沿OD翻折,点C的对应点为![]() ,连接
,连接![]() ,并取
,并取![]() 的中点F,连接PF,当四边形AOCP的面积等于
的中点F,连接PF,当四边形AOCP的面积等于![]() 时,求PF的最大值;
时,求PF的最大值;
(2)如图2,将直线AC绕点O顺时针方向旋转α度![]() ,分别与x轴和直线BC相交于点S和点R,当
,分别与x轴和直线BC相交于点S和点R,当![]() 是等腰三角形时,直接写出α的度数.
是等腰三角形时,直接写出α的度数.
【答案】(1)PF的最大值是![]() ;(2)
;(2)![]() 的度数:
的度数:![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)设P(m,-m+6),连接OP.根据S四边形AOCP=S△AOP+S△OCP=![]() ,构建方程求出点P坐标,取OB的中点Q,连接QF,QP,求出FQ,PQ,根据PF≤PQ+QF求解即可.
,构建方程求出点P坐标,取OB的中点Q,连接QF,QP,求出FQ,PQ,根据PF≤PQ+QF求解即可.
(2)分四种情形:①如图2-1中,当RS=RB时,作OM⊥AC于M.②如图2-2中,当BS=BR时,③如图2-3中,当SR=SB时,④如图2-4中,当BR=BS时,分别求解即可解决问题.
解:(1)在![]() 中,当
中,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ﹒
﹒
∴![]() ,
,![]()
设![]() ,连接OP
,连接OP
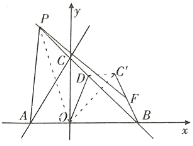
∴![]()
∴![]()
∴![]() ∴
∴![]()
取OB的中点Q,连接FQ,PQ
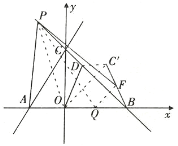
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]() ∴
∴![]()
又∵点F是![]() 的中点,
的中点,
∴![]()
∵![]()
所以PF的最大值是![]()
(2)①如图2-1中,当RS=RB时,作OM⊥AC于M.
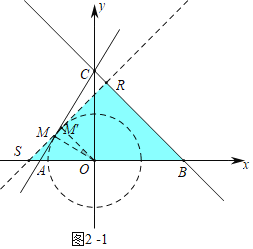
∵tan∠OAC=![]() =
=![]() ,
,
∴∠OAC=60°,
∵OC=OB=6,
∴∠OBC=∠OCB=45°,
∵∠OM′S=∠BRS=90°,
∴OM′∥BR,
∴∠AOM′=∠OBC=45°,
∵∠AOM=30°,
∴α=45°-30°=15°.
②如图2-2中,当BS=BR时,易知∠BSR=22.5°,
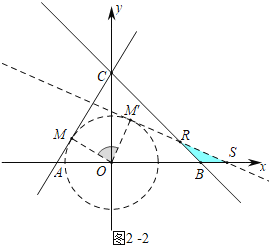
∴∠SOM′=90°-22.5°=67.5°,
∴α=∠MOM′=180°-30°-67.5°=82.5°
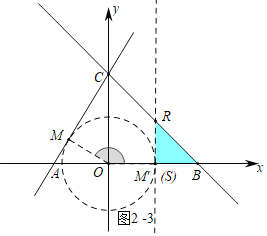
③如图2-3中,当SR=SB时,α=180°-30°=150°.
④如图2-4中,当BR=BS时,α=150°+(90°-67.5°)=172.5°.
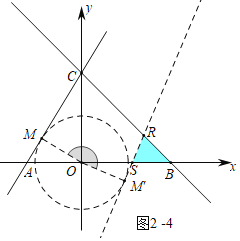
综上所述,满足条件的α的值为15°或82.5°或150°或172.5°.


科目:初中数学 来源: 题型:
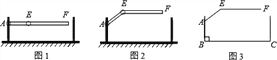
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点![]() 当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示
当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示![]() 栏杆宽度忽略不计
栏杆宽度忽略不计![]() ,其中
,其中![]() 米,那么适合该地下车库的车辆限高标志牌为
米,那么适合该地下车库的车辆限高标志牌为
(参考数据:![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
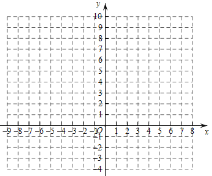
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于(﹣1)n= ,所以我们通常把(﹣1)n称为符号系数.
,所以我们通常把(﹣1)n称为符号系数.
(1)观察下列单项式:﹣![]() ,…按此规律,第5个单项式是 ,第n个单项式是 .
,…按此规律,第5个单项式是 ,第n个单项式是 .
(2)![]() 的值为 ;
的值为 ;
(3)你根据(2)写出一个当n为偶数时值为2,当n为奇数时值为0的式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
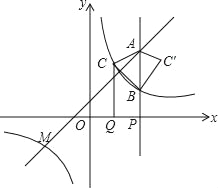
【题目】如图,点M(﹣3,m)是一次函数y=x+1与反比例函数y=![]() (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点.
(1)求反比例函数表达式;
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②当a的值为 时,△AMC与△AMC′的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
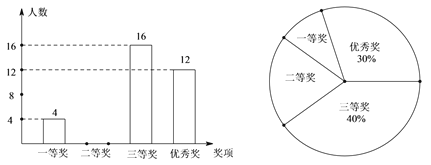
【题目】某中学在全校学生中开展了“地球—我们的家园”为主题的环保征文比赛,评选出一、二、三等奖和优秀奖。根据奖项的情况绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)求校获奖的总人数,并把条形统计图补充完整;
(2)求在扇形统计图中表示“二等奖” 的扇形的圆心角的度数;
(3)获得一等奖的4名学生中有3男1女,现打算从中随机选出2名学生参加颁奖活动,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com