
【题目】若![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() ,
,![]() 和系数
和系数![]() ,
,![]() ,
,![]() 有如下关系:
有如下关系:![]() ,
,![]() ,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
已知![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值,若不存在,请你说明理由;
的值,若不存在,请你说明理由;
(2)若![]() ,求
,求![]() 的值和此时方程的两根.
的值和此时方程的两根.
【答案】(1)存在,12(2)![]() ,
,![]() ;
;![]() ,
,![]()
【解析】
(1)先根据根的判别式得到m的取值范围为m≥0且m≠3,再根据根与系数的关系得x1+x2=![]() ,x1x2=
,x1x2=![]() ,然后利用-x1+x1x2=4+x2得
,然后利用-x1+x1x2=4+x2得![]() ,再解关于m的方程即可;
,再解关于m的方程即可;
(2)先利用完全平方公式变形得到(x1-x2)2=3,即(x1+x2)2-4x1x2=3,再把![]() ,
,![]() ,代入得到(-
,代入得到(-![]() )2-4×
)2-4×![]() =3,解得m1=1,m2=9,
=3,解得m1=1,m2=9,
然后分别把m的值代入原方程,并且利用公式法解方程.
(1)存在.
∵![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,
的两个实数根,
∴![]() 且
且![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() 且
且![]() ,
,
根据根与系数的关系得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,原方程变形为
时,原方程变形为![]() ,解得
,解得![]() ,
,![]() ;
;
当![]() 时,原方程变形为
时,原方程变形为![]() ,解得
,解得![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
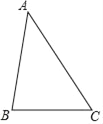
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°,AB的垂直平分线分别与AC、AB交于点D、E.
(1)在图中作出AB的垂直平分线DE,并连接BD.
(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装有红、黄、蓝三种颜色的球(除颜色以外,其余都相同),其中红球2个,黄球2个,从中随机摸出一个球是蓝色球的概率为![]() .
.
(1)求袋子里蓝色球的个数;
(2)甲、乙两人分别从袋中摸出一个球(不放回),求摸出的两个球中一个是红球一个是黄球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.
(1)分别求出当2≤x≤4时,三个函数:y=2x+1,y=![]() ,y=2(x﹣1)2+1的最大值和最小值;
,y=2(x﹣1)2+1的最大值和最小值;
(2)若y=![]() 的值不大于2,求符合条件的x的范围;
的值不大于2,求符合条件的x的范围;
(3)若y=![]() ,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;
,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;
(4)y=2(x﹣m)2+m﹣2,当2≤x≤4时有最小值为1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
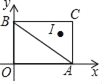
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0..其中正确的结论有:

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
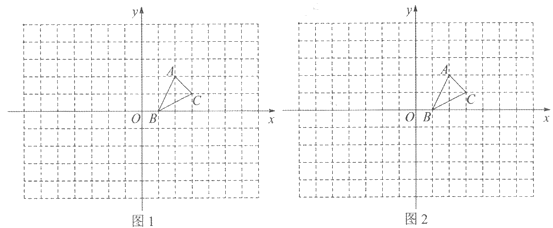
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)在图l中画出△ABC关于x轴对称的△A1B1C1;
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可). 直接写出点A的对应点A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
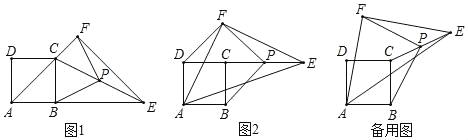
【题目】等腰Rt△AEF(其中FA=FE,∠AFE=90°,AE=6)与正方形ABCD(其中AB=2)有共同的顶点A,连接CE,点P是CE的中点,连接PB,PF.
(1)如图1,当点E恰好落在AB的延长线上时,请求出∠BPF的度数,并求出PB与PF的长.
(2)如图2,把等腰Rt△AEF绕点A旋转,当点E恰好在DC的延长线上时,
①请求出PC的长.
②判断PB与PF的数量关系与位置关系,并说明理由.
(3)把等腰Rt△AEF绕点A由如图1所示的位置逆时针旋转180°,在旋转过程中,点P的位置也随之改变,请思考点P运动的轨迹,直接写出点P运动的路程____.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com