
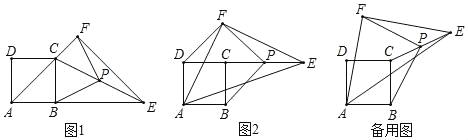
【题目】等腰Rt△AEF(其中FA=FE,∠AFE=90°,AE=6)与正方形ABCD(其中AB=2)有共同的顶点A,连接CE,点P是CE的中点,连接PB,PF.
(1)如图1,当点E恰好落在AB的延长线上时,请求出∠BPF的度数,并求出PB与PF的长.
(2)如图2,把等腰Rt△AEF绕点A旋转,当点E恰好在DC的延长线上时,
①请求出PC的长.
②判断PB与PF的数量关系与位置关系,并说明理由.
(3)把等腰Rt△AEF绕点A由如图1所示的位置逆时针旋转180°,在旋转过程中,点P的位置也随之改变,请思考点P运动的轨迹,直接写出点P运动的路程____.(结果保留π)
【答案】(1)∠FPB=90°;PF=![]() ;BP=
;BP=![]() ;(2)①CP=2
;(2)①CP=2![]() ﹣1;②PF⊥BP,PF=BP;(3)3π
﹣1;②PF⊥BP,PF=BP;(3)3π
【解析】
(1)根据勾股定理可求CE=2![]() ,根据直角三角形斜边上的中线等于斜边的一半,可求BP=PF=
,根据直角三角形斜边上的中线等于斜边的一半,可求BP=PF=![]() ,∠FPB=2∠FEA=90°;
,∠FPB=2∠FEA=90°;
(2)①由勾股定理可求DE的长,即可求CE的长,由P点是CE中点可求CP的长;
②过点E作GE∥BC,交BP的延长线于G,连接FG,BF,由题意可证△GEP≌△BCP,可得BP=GP,GE=BC,即可证△AFB≌△EFG,可得BF=FG,∠AFB=∠EFG,可得△BFG是等腰直角三角形,则PF⊥BP,PF=BP;
③以点A为原点,AB为x轴,AD为y轴建立直角坐标系,连接AC,BD交于点G.由题意可求点G(1,1),点C(2,2)设E(x,y),由AE=6,可得x2+y2=36,则可求点P(![]() ,
,![]() ),根据两点公式可求GP=3,即点P在以G为圆心,半径为3的圆上运动,即可求点P运动的路程.
),根据两点公式可求GP=3,即点P在以G为圆心,半径为3的圆上运动,即可求点P运动的路程.
解:(1)∵FA=FE,∠AFE=90°
∴∠FEA=45°
∵AB=2,AE=6
∴BE=4
在Rt△BCE中,CE=![]() =2
=2![]()
∵∠CFE=90°,点P是CE中点,
∴PE=PF=CP=![]() ,
,
∴∠PEF=∠PFE
即∠FPC=2∠FEP
∵∠CBE=90°,点P是CE中点
∴BP=PE=![]() ,
,
∴∠PEB=∠PBE
∴∠CPB=2∠PEB
∵∠FPB=∠FPC+∠CPB=2∠FEP+2∠PEB=2∠FEB
∴∠FPB=90°
(2)①∵AE=6,AD=2
∴由勾股定理可得:DE=![]() =4
=4![]() ,
,
∴CE=DE﹣DC=4![]() ﹣2
﹣2
∵点P是CE中点
∴CP=![]() =2
=2![]() ﹣1
﹣1
②过点E作GE∥BC,交BP的延长线于G,连接FG,BF,
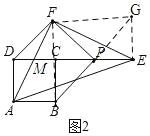
∵GE∥BC
∴∠BCE=∠GEP=90°且CP=PE,∠BPC=∠GPE
∴△GEP≌△BCP(AAS)
∴BP=GP,GE=BC
∵CD∥AB
∴∠FAB=∠FME
∵∠FME+∠FED=90°,∠FED+∠FEG=90°
∴∠FME=∠FEG
∴∠FAB=∠FEG,且GE=CB=AB,AF=EF
∴△AFB≌△EFG(SAS)
∴BF=FG,∠AFB=∠EFG
∵∠AFB+∠BFE=90°
∴∠BFE+∠EFG=90°
∴∠BFG=90°且BF=FG
∴△BFG是等腰直角三角形且BP=PG
∴PF⊥BP,PF=BP
(3)以点A为原点,AB为x轴,AD为y轴建立直角坐标系,连接AC,BD交于点G.
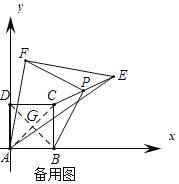
∵四边形ABCD是正方形,AB=2
∴AB=2=BC=CD=AD,AG=CG
∴点C(2,2)且点A(0,0)
∴点G(1,1)
设E(x,y)
∵AE=6
∴x2+y2=36
∵点P是CE的中点,且点C(2,2),点E(x,y)
∴点P(![]() ,
,![]() ),
),
∴GP=![]() =
=![]() =3
=3
∴点P运动的路程=![]() =3π
=3π
故答案为:3π


科目:初中数学 来源: 题型:
【题目】若![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() ,
,![]() 和系数
和系数![]() ,
,![]() ,
,![]() 有如下关系:
有如下关系:![]() ,
,![]() ,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
,把它们称为一元二次方程根与系数关系定理,请利用此定理解答一下问题:
已知![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根.
的两个实数根.
(1)是否存在实数![]() ,使
,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的值,若不存在,请你说明理由;
的值,若不存在,请你说明理由;
(2)若![]() ,求
,求![]() 的值和此时方程的两根.
的值和此时方程的两根.
查看答案和解析>>
科目:初中数学 来源: 题型:
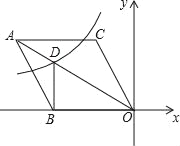
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3![]() ),反比例函数y=
),反比例函数y=![]() 的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是_____.
的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
的图像分别交y轴、x轴交于点A、B,点P从点B出发,沿射线BA以每秒1个单位的速度出发,设点P的运动时间为t秒.
(1)点P在运动过程中,若某一时刻,△OPA的面积为6,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?(只需写出t的值,无需解答过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
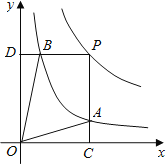
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
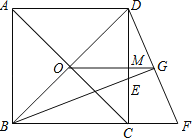
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8-4![]() ,求正方形ABCD的面积?
,求正方形ABCD的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的二次函数y=2sin![]() x2-(4sin
x2-(4sin![]() +
+![]() )x-sin
)x-sin![]() +
+![]() ,其中
,其中![]() 为锐角,则:①当a为30°时,函数有最小值﹣
为锐角,则:①当a为30°时,函数有最小值﹣![]() ;②函数图象与坐标轴可能有三个交点,并且当a为45°时,连接这三个交点所围成的三角形面积小于1;③当a<60°时,函数在x>1时,y随x的增大而增大;④无论锐角a怎么变化,函数图象必过定点.其中正确的结论有( )
;②函数图象与坐标轴可能有三个交点,并且当a为45°时,连接这三个交点所围成的三角形面积小于1;③当a<60°时,函数在x>1时,y随x的增大而增大;④无论锐角a怎么变化,函数图象必过定点.其中正确的结论有( )
A. ①② B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5…,过A1、A2、A3、A4、A5…分别作x轴的垂线与反比例函数y=![]() 的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
的图象交于点P1、P2、P3、P4、P5…,并设△OA1P1、△A1A2P2、△A2A3P3…面积分别为S1、S2、S3…,按此作法进行下去,则Sn的值为 (n为正整数).
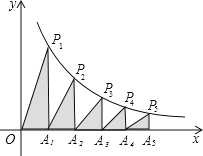
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com