
分析 (1)由小莹选修两门课程的可能有三种:“国学”和“拉丁舞”,“国学”和“机器人”,“拉丁舞”和“机器人”,其中含有国学的有两种:“国学”和“机器人”,“拉丁舞”和“国学”.直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两人选修同一门课程的情况,再利用概率公式即可求得答案.
解答 解:(1)∵小莹选修两门课程的可能有三种:“国学”和“拉丁舞”,“国学”和“机器人”,“拉丁舞”和“机器人”,其中含有国学的有两种:“国学”和“机器人”,“拉丁舞”和“国学”.
∴小莹选修两门课程中含有国学的概率为:$\frac{2}{3}$;
(2)画树状图得: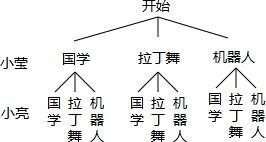
∵共有9种等可能的结果,两人选修同一门课程的有3种情况,
∴小莹和小亮选修同一门课程的概率为:$\frac{3}{9}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
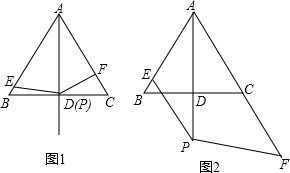
 如图,点B、E、C、F在同一直线上,AC=DF,BE=CF,只要再找出边AC=边ED,或∠ACB=∠F,或AC∥DF,就可以证得△DEF≌△ABC.
如图,点B、E、C、F在同一直线上,AC=DF,BE=CF,只要再找出边AC=边ED,或∠ACB=∠F,或AC∥DF,就可以证得△DEF≌△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
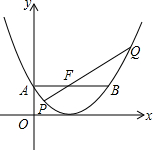 如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).
如图,已知抛物线C1:y1=$\frac{1}{4}$x2-x+1,点F(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | 只有(3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,2 | B. | 2,3 | C. | 4,1 | D. | 2、2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com