
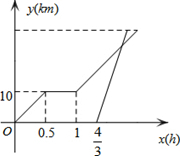
 周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.
周末,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后,按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知妈妈驾车速度是小明的3倍.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据速度=路程÷时间可得出小明骑车的速度,由与x轴平行的线段端点的横坐标可得知小明在甲地玩了0.5小时,故①不成立;根据小明的速度可求出妈妈的速度,结合妈妈出发的时间可算出此时小明离家的路程,由时间=路程÷速度差即可得知妈妈追上小明的时间,加上妈妈出发的时间可得出②成立;由妈妈追上小明的时间结合妈妈的速度可求出妈妈追上小明时离家的距离从而得出③成立;设总路程为S,根据从相遇到到达终点妈妈比小明少用10分钟,即可列出关于S的一元一次方程,解方程求出S即可判断出④成立.结合上面各结论可得知结论.
解答 解:小明骑车速度为10÷0.5=20(km/h),
1-0.5=0.5(h),即①不成立;
妈妈驾车的速度为20×3=60(km/h),
妈妈出发时小明离家的路程为10+($\frac{4}{3}$-1)×20=$\frac{50}{3}$(km),
妈妈追上小明需要的时间为$\frac{50}{3}$÷(60-20)=$\frac{5}{12}$(h),
此时小明离家时间为$\frac{4}{3}$+$\frac{5}{12}$=$\frac{7}{4}$(h),即②成立;
妈妈追上小明时离家的距离为60×$\frac{5}{12}$=25(km),③成立;
10分钟=$\frac{1}{6}$小时,
设总路程为S,由题意可知:
$\frac{S-25}{60}$=$\frac{S-25}{20}$-$\frac{1}{6}$,
解得:S=30.
从家到乙地的距离为30km,④成立.
故选C.
点评 本题考查了一次函数的应用,解题的关键是结合图形利用各数量间的关系求出未知量再与4个说法进行比较.本题属于基础题,难度不大,解决该题型题目时,结合图形是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-a|=a | B. | a2•a3=a6 | C. | ${({-2})^{-1}}=-\frac{1}{2}$ | D. | ($\sqrt{3}$)0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
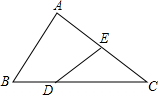 如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)
如图,在△ABC中,点D在边BC上,且DC=2BD,点E是边AC的中点,设$\overrightarrow{BC}=\vec a,\overrightarrow{AC}=\vec b$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$;(用不$\vec a、\vec b$的线性组合表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com