
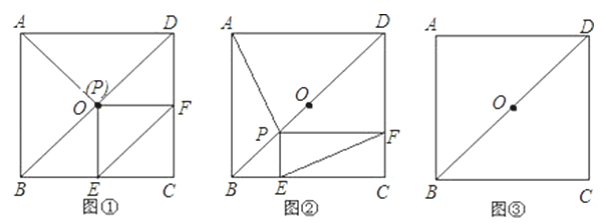
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
【答案】(1)AP=EF,AP⊥EF,理由见解析;(2)仍成立,理由见解析;(3)仍成立,理由见解析;
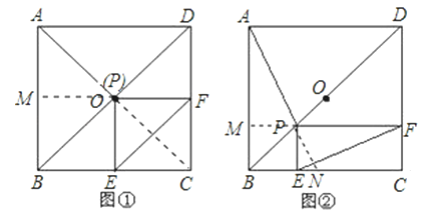
【解析】试题分析:(1)正方形中容易证明∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,利用AAS证明△AMO≌△FOE.(2) (3)按照(1)中的证明方法证明△AMP≌△FPE(SAS),结论依然成立.
试题解析:
(1)AP=EF,AP⊥EF,理由如下:
连接AC,则AC必过点O,延长FO交AB于M;
∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,
∴四边形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE(AAS),
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
(2)题(1)的结论仍然成立,理由如下:
延长AP交BC于N,延长FP交AB于M;
∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB﹣BM=AM,BC﹣BE=EC=PF,且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE(SAS),
∴AP=EF,∠APM=∠FPN=∠PEF,
∵∠PEF+∠PFE=90°,∠FPN=∠PEF,
∴∠FPN+∠PFE=90°,即AP⊥EF,
故AP=EF,且AP⊥EF.
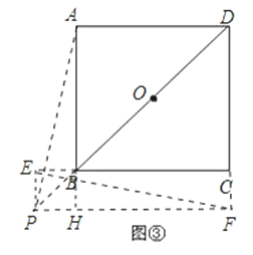
(3)题(1)(2)的结论仍然成立;
如右图,延长AB交PF于H,证法与(2)完全相同.


科目:初中数学 来源: 题型:
【题目】用5个棱长为1的正方体组成如图所示的几何体.
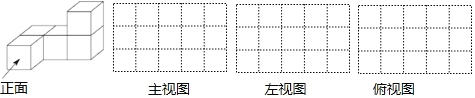
(1)该几何体的体积是多少立方单位,表面积是多少平方单位(包括底面积);
(2)请在方格纸中用实线画出它的三个视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
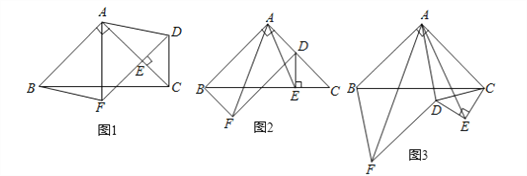
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
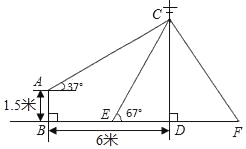
【题目】如图,在电线杆CD处引拉线CE,CF固定电线杆,拉线CE和地面所成的角∠CED=67°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为37°,求拉线CE的长(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tsn37°≈
,tsn37°≈![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
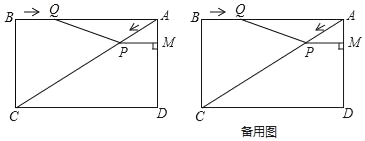
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
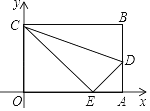
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP=![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,a、b、c 均为非零实数,且 a>b>c,关于 x 的一元二次方程ax2 bx c 0 有两个实数根 x1和 2。(1)4a +2b +c _____0,a _____0,c _________0(填“>”,“=”,“<”)(2)方程 ax2 bx c 0 的另一个根 x1=_______(用含 a、c 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校初一(2)班组织学生从A地到B地步行野营,匀速前进,该班师生共56人,每8人排成一排,相邻两排之间间隔1米,途中经过一座桥CD,队伍从开始上桥到刚好完全离开桥共用了150秒,当队尾刚好走到桥的一端D处时,排在队尾的游班长发现小蒋还在桥的另一端C处拍照,于是以队伍1.5倍的速度返回去找小萍,同时队伍仍按原速度继续前行,30秒后,小蒋发现游班长返回来找他,便立刻以2.1米/秒的速度向游班长方向行进,小蒋行进40秒后与游班长相遇,相遇后两人以队伍2倍的速度前行追赶队伍.
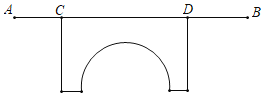
(1)初一(2)班的队伍长度为 米;
(2)求班级队伍行进的速度(列一元一次方程解决问题);
(3)请问:游班长从D处返回赵小萍开始到他们两人追上队首的刘老师一共用了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com