
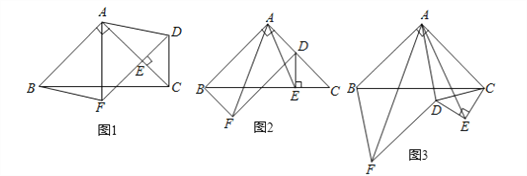
����Ŀ����ͼ1���ڵ���Rt��ABC������BAC=90������E��AC�ϣ��Ҳ����A��C�غ���������ABC���ⲿ������Rt��CED��ʹ��CED=90��������AD���ֱ���AB��ADΪ�ڱ���ƽ���ı���ABFD������AF��
��1����֤����AEF�ǵ���ֱ����������
��2����ͼ2������CED�Ƶ�C��ʱ����ת������E���߶�BC��ʱ������AE����֤��AF=![]() AE��
AE��
��3����ͼ3������CED�Ƶ�C������ʱ����ת����ƽ���ı���ABFDΪ����������CED����ABC���·�ʱ����AB=2![]() ��CE=2�����߶�AE�ij���
��CE=2�����߶�AE�ij���
���𰸡���1���𰸼���������2���𰸼���������3��4![]() ��
��
�������������������1������AE=EF����DEC=��AEF=90�㣬����֤����AEF�ǵ���ֱ����������
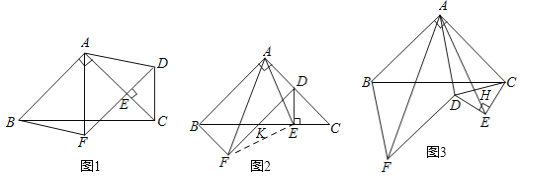
��2������EF��DF��BC��K����֤����EKF�ա�EDA����֤����AEF�ǵ���ֱ�������μ��ɵó�������
��3����AD=AC=ABʱ���ı���ABFD�������������EH=DH=CH=![]() ��Rt��ACH����AH=3
��Rt��ACH����AH=3![]() �����ɵõ�AE=AH+EH=4
�����ɵõ�AE=AH+EH=4![]() ��
��
���������������1����ͼ1�����ı���ABFD��ƽ���ı�������AB=DF����AB=AC����AC=DF����DE=EC����AE=EF���ߡ�DEC=��AEF=90�㣬���AEF�ǵ���ֱ����������
��2����ͼ2������EF��DF��BC��K�����ı���ABFD��ƽ���ı�������AB��DF�����DKE=��ABC=45�㣬���EKF=180�㩁��DKE=135�㣬EK=ED���ߡ�ADE=180�㩁��EDC=180�㩁45��=135�㣬���EKF=��ADE���ߡ�DKC=��C����DK=DC����DF=AB=AC����KF=AD������EKF�͡�EDA���� 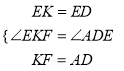 �����EKF�ա�EDA��SAS������EF=EA����KEF=��AED�����FEA=��BED=90�㣬���AEF�ǵ���ֱ������������AF=
�����EKF�ա�EDA��SAS������EF=EA����KEF=��AED�����FEA=��BED=90�㣬���AEF�ǵ���ֱ������������AF=![]() AE��
AE��
��3����ͼ3����AD=AC=ABʱ���ı���ABFD����������AE��CD��H������AD=AC��ED=EC���ɵ�AE��ֱƽ��CD����CE=2����EH=DH=CH=![]() ��Rt��ACH����AH=
��Rt��ACH����AH=![]() =3
=3![]() ����AE=AH+EH=4
����AE=AH+EH=4![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
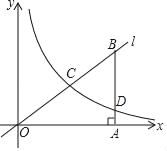
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬����ԭ���ֱ��l�뷴��������![]() ��x��0����ͼ���ڵ�C��B��ֱ��l�ϵĵ㣬����B��BA��x�ᣬ����Ϊ��A����C��OB�е㣬��֪OA=4��BD=3��
��x��0����ͼ���ڵ�C��B��ֱ��l�ϵĵ㣬����B��BA��x�ᣬ����Ϊ��A����C��OB�е㣬��֪OA=4��BD=3��
��1���ú�k�Ĵ���ʽ����ʾD�������Ϊ_____��
��2�����������Ľ���ʽ��
��3������CD�����ı���OADC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��A��B��1�����A��B�ǹ���1�ĵ�λ��.
(1)3��______�ǹ���1�ĵ�λ����x��3��______�ǹ���1�ĵ�λ��.(��һ����x��ʽ��)
(2)��A��3x(x+2)��1��![]() ���ж�A��B�Ƿ��ǹ���1�ĵ�λ������˵������.
���ж�A��B�Ƿ��ǹ���1�ĵ�λ������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ��������ǰ�����ļ�����2019�꿪ʼ�������ɼ�����һ����ԭʼ�ּ����п��ܷ֡�ijУΪ��Ӧ�µ��п�Ҫ����Ϊ����������һ���������ġ�ѧУ�������϶���һ��ijƷ��������������ڲ�����è�����������ÿ������150Ԫ������ÿ������30Ԫ������A��B����������ṩ���ʷ�������˸��Ե��Żݷ�����
A���꣺��һ��������һ��������
B���꣺����������������۵�90%���
��֪Ҫ��������40��������x����x��40��
��1������A���깺���踶�� Ԫ���ú�x�Ĵ���ʽ��ʾ��.
����B���깺���踶�� Ԫ���ú�x�Ĵ���ʽ��ʾ��.
��2����x=100ʱ��ͨ������˵����ʱ���ļ����깺���Ϊ���㣿
��3����x=100ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
�������踶�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֳ�Ҫ����һ��������һ�������µ���ֲ�ɻ��ʣ�����ֲ�����е�ͳ�ƽ�����±���ʾ��
��ֲ������n/�� | 500 | 1000 | 2000 | 4000 | 7000 | 10000 | 12000 | 15000 |
�ɻ������m/�� | 423 | 868 | 1714 | 3456 | 6020 | 8580 | 10308 | 12915 |
�ɻ��Ƶ�� | 0.846 | 0.868 | 0.857 | 0.864 | 0.860 | 0.858 | 0.859 | 0.861 |
�ڴ������£����Ƹ���������ֲ�ɻ�ĸ���Ϊ_________________����ȷ��![]() ���������ֳ���ʹ�ɻ�������ﵽ4.3��ã��������Ҫ��ֲ��������_________���.
���������ֳ���ʹ�ɻ�������ﵽ4.3��ã��������Ҫ��ֲ��������_________���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ�����ס������������ˮ��3�����Ϊ�˿���ˮ���볤���������ͬһ������������������ֱ������ȡ��![]() ��������в�������������ǵij���
��������в�������������ǵij���![]() ����λ��cm�����������ݣ��볤�������������������ͷ���.��������˲�����Ϣ.
����λ��cm�����������ݣ��볤�������������������ͷ���.��������˲�����Ϣ.
a.���������볤��Ƶ���ֲ�ͳ�Ʊ����±���ʾ������������
���������볤Ƶ���ֲ���
����/ | Ƶ�� | Ƶ�� |
| 4 | 0.08 |
| 9 | 0.18 |
|
| |
| 11 | 0.22 |
|
| 0.20 |
| 2 | |
�ϼ� | 50 | 1.00 |
b.���������볤��Ƶ���ֲ�ֱ��ͼ��ͼ��ʾ��
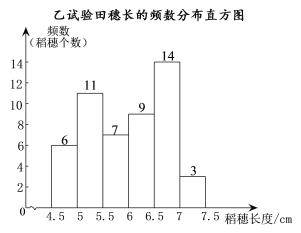
c.���������볤��![]() ��һ����ǣ�
��һ����ǣ�
6.3 6.4 6.3 6.3 6.2 6.2 6.1 6.2 6.4
d.�ס����������볤��ƽ��������λ�����������������£���2����
������ | ƽ���� | ��λ�� | ���� | ���� |
�� | 5.924 | 5.8 | 5.8 | 0.454 |
�� | 5.924 |
| 6.5 | 0.608 |
����������Ϣ���ش��������⣺
��1������![]() ��ֵΪ ��
��ֵΪ ��![]() ��ֵΪ ��
��ֵΪ ��
��2������![]() ��ֵΪ ��
��ֵΪ ��
��3���ڴ˴ο����У��������������ȣ����ȶ����������� ��
A���� B���� C�����ƶ�
��4�����볤��![]() ��Χ�ڵĵ���Ϊ�����á�������Ƽ����������С����á���ˮ��ԼΪ �����
��Χ�ڵĵ���Ϊ�����á�������Ƽ����������С����á���ˮ��ԼΪ �����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������6�֣�ij��˾����ij��ѧѧ�����价����Ʒ���˽�����������ȡ��У����ѧ�������ʾ�������֡��dz��˽⡱�����Ƚ��˽⡱����һ���˽⡱�������˽⡱�������ͣ��ֱ��ΪA��B��C��D.���ݵ����������������в�������ͳ��ͼ. 
��1�������ʾ������������ ��ѧ��������ͳ��ͼ��m= .
��2�������������Ϣ��ȫ����ͳ��ͼ��
��3������У��1000��ѧ��������ѡ�dz��˽⡱�����Ƚ��˽⡱��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У���O�ǶԽ���DB���е㣬��P��DB����ֱ���ϵ�һ�����㣬PE��BC��E��PF��DC��F��
��1������P���O�غ�ʱ����ͼ�٣����²�AP��EF��������λ�ù�ϵ����֤����Ľ��ۣ�
��2������P���߶�DB�ϣ������D��O��B�غϣ�ʱ����ͼ�ڣ���̽����1���еĽ����Ƿ��������������д��֤�����̣�������������˵�����ɣ�
��3������P��DB�ij��ӳ�����ʱ���뽫ͼ�۲������������жϣ�1���еĽ����Ƿ��������������ֱ��д�����ۣ�������������д����Ӧ�Ľ��ۣ�
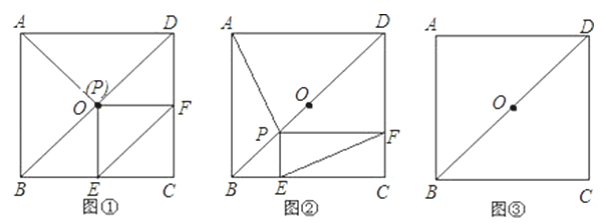
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�ڽ�����O������O�İ뾶Ϊ6��sinA=![]() ����BC�ij���
����BC�ij���

���𰸡�BC=8��
�����������������ͨ���������߹���ֱ�������Σ����������Ǻ���֪ʶ������⣮
�������������O��ֱ��CD������BD����CD=2��6=12.
��![]()
��![]()
��![]()

�㾦��ֱ�����Ե�Բ�ܽ���ֱ��.
�����͡������
��������
22
����Ŀ����ͼ��һ�κ���y=k1x+b�뷴��������y=![]() ��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽk1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P��p��y1����Q����2��y2���Ǻ���y=![]() ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��
ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com