
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
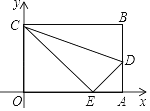
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP=![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)E(8,0);
(2)y=﹣![]() x+6
x+6
(3)①54;②点P的坐标为(6,0)或(﹣6,0).
【解析】
(1)根据折叠的性质知CE=CB=10.在在直角△COE中,由勾股定理求得OE=8;
(2)根据OC=6知C(0,6),由折叠的性质与勾股定理,求得D(10,![]() ),利用待定系数法求CD所在直线的解析式;
),利用待定系数法求CD所在直线的解析式;
(3)①根据F(18,0),即可求得△COF的面积;②设P(x,0),依S△OCP=![]() S△CDE得
S△CDE得![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,求得x的值,即可得出点P的坐标.
×|x|×6=18,求得x的值,即可得出点P的坐标.
(1)如图,
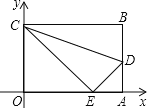
∵四边形ABCD是长方形,
∴BC=OA=10,∠COA=90°,
由折叠的性质知,CE=CB=10,
∵OC=6,
∴在直角△COE中,由勾股定理得OE=![]() =8,
=8,
∴E(8,0);
(2)设CD所在直线的解析式为y=kx+b(k≠0),
∵C(0,6),
∴b=6,
设BD=DE=x,
∴AD=6-x,AE=OA-OE=2,
由勾股定理得AD2+AE2=DE2
即(6-x)2+22=x2,
解得x=![]() ,
,
∴AD=6-![]() =
=![]() ,
,
∴D(10,![]() ),
),
代入y=kx+6 得,k=-![]() ,
,
故CD所在直线的解析式为:y=-![]() x+6;
x+6;
(3)①在y=-![]() x+6中,令y=0,则x=18,
x+6中,令y=0,则x=18,
∴F(18,0),
∴△COF的面积=![]() ×OF×OC=
×OF×OC=![]() ×18×6=54;
×18×6=54;
②在x轴上存在点P,使得S△OCP=![]() S△COF,
S△COF,
设P(x,0),依题意得
![]() ×OP×OC=
×OP×OC=![]() ×54,即
×54,即![]() ×|x|×6=18,
×|x|×6=18,
解得x=±6,
∴在x轴上存在点P,使得S△OCP=![]() S△COF,点P的坐标为(6,0)或(-6,0).
S△COF,点P的坐标为(6,0)或(-6,0).


科目:初中数学 来源: 题型:
【题目】定义:若A﹣B=1,则称A与B是关于1的单位数.
(1)3与______是关于1的单位数,x﹣3与______是关于1的单位数.(填一个含x的式子)
(2)若A=3x(x+2)﹣1,![]() ,判断A与B是否是关于1的单位数,并说明理由.
,判断A与B是否是关于1的单位数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为A、B、C、D.根据调查结果绘制了如下尚不完整的统计图. 
(1)本次问卷共随机调查了 名学生,扇形统计图中m= .
(2)请根据数据信息补全条形统计图;
(3)若该校有1000名学生,估计选择“非常了解”、“比较了解”共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
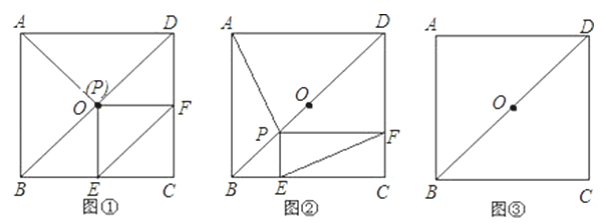
【题目】正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上(不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
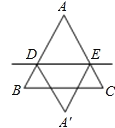
【题目】如图,等边三角形ABC的边长为3,D、E分别是AB、AC上的点,且AD=AE=2,将△ADE沿直线DE折叠,点A的落点记为A′,则四边形ADA′E的面积S1与△ABC的面积S2之间的关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)类比计算
①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
⑤ ;
(2)规律提炼
写出第n个式子(用含字母n的式子表示).
(3)问题解决
求12+22+33+42+…+592+602的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.

【答案】BC=8.
【解析】试题分析:通过作辅助线构成直角三角形,再利用三角函数知识进行求解.
试题解析:作⊙O的直径CD,连接BD,则CD=2×6=12.
∵![]()
∴![]()
∴![]()

点睛:直径所对的圆周角是直角.
【题型】解答题
【结束】
22
【题目】如图,一次函数y=k1x+b与反比例函数y=![]() 的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=![]() 图象上的两点,且y1≥y2,求实数p的取值范围.
图象上的两点,且y1≥y2,求实数p的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的知识竞赛活动中,老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表:
得分(分) 人数(人) 班级 | 50 | 60 | 70 | 80 | 90 | 100 |
一班 | 2 | 5 | 10 | 13 | 14 | 6 |
二班 | 4 | 4 | 16 | 2 | 12 | 12 |
(1)现已知一班和二班的平均分相同,请求出其平均分.
(2)请分别求出这两班的中位数和众数,并进一步分析这两个班级在这次竞赛中成绩的情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com