
【题目】(1)类比计算
①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
⑤ ;
(2)规律提炼
写出第n个式子(用含字母n的式子表示).
(3)问题解决
求12+22+33+42+…+592+602的值.
【答案】(1)5×6×11﹣4×5×9.(2)6n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).(3)73810.
【解析】
(1)⑤根据题目中前几个式子的规律即可得结论6×52=5×6×11﹣4×5×9;
(2)根据前边几个式子的规律即可写出第n个式子6×n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).;
(3)先变形为![]() (6×12+6×22+6×32+6×42+…+6×592+6×602),再利用(2)中求得的规律式展开,即可求解.
(6×12+6×22+6×32+6×42+…+6×592+6×602),再利用(2)中求得的规律式展开,即可求解.
解:(1)∵①6×12=1×2×3;
②6×22=2×3×5﹣1×2×3;
③6×32=3×4×7﹣2×3×5;
④6×42=4×5×9﹣3×4×7;
∴⑤6×52=5×6×11﹣4×5×9
故答案为6×52=5×6×11﹣4×5×9.
(2)根据以上算式,得
第n个式子为6n2=n(n+1)(2n+1)﹣(n﹣1)n(2n﹣1).
(3)12+22+33+42+…+592+602
=![]() (6×12+6×22+6×32+6×42+…+6×592+6×602)
(6×12+6×22+6×32+6×42+…+6×592+6×602)
=![]() (1×2×3+2×3×5﹣1×2×3+3×4×7﹣2×3×5+4×5×9﹣3×4×7+…+59×60×119﹣58×59×117+60×61×121﹣59×60×119)
(1×2×3+2×3×5﹣1×2×3+3×4×7﹣2×3×5+4×5×9﹣3×4×7+…+59×60×119﹣58×59×117+60×61×121﹣59×60×119)
=![]() ×60×61×121
×60×61×121
=73810.
答:12+22+33+42+…+592+602的值为73810.


科目:初中数学 来源: 题型:
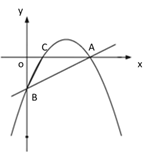
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
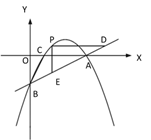
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
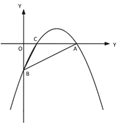
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
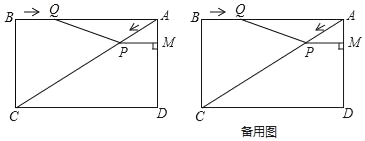
【题目】已知:如图,在矩形ABCD中,AC是对角线,AB=8cm,BC=6cm.点P从点A出发,沿AC方向匀速运动,速度为2cm/s,同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s.过点P作PM⊥AD于点M,连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,点Q在线段AC的中垂线上;
(2)写出四边形PQAM的面积为S(cm2)与时间t的函数关系式;
(3)是否存在某一时刻t,使S四边形PQAM:S矩形ABCD=9:50?若存在,求出t的值;若不存在,请说明理由;
(4)当t为何值时,△APQ与△ADC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,四边形OABC是长方形,O为原点,点A在x轴上,点C在y轴上且A(10,0),C(0,6),点D在AB边上,将△CBD沿CD翻折,点B恰好落在OA边上点E处.
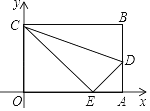
(1)求点E的坐标;
(2)求折痕CD所在直线的函数表达式;
(3)请你延长直线CD交x轴于点F. ①求△COF的面积;
②在x轴上是否存在点P,使S△OCP=![]() S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
S△COF?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 的两边
的两边![]() 、
、![]() 的长分别是关于x的一元二次方程
的长分别是关于x的一元二次方程![]() 的两个实数根,第三边
的两个实数根,第三边![]() 的长为5.
的长为5.
(1)当![]() 为何值时,
为何值时, ![]() 是直角三角形;
是直角三角形;
(2)当![]() 为何值时,
为何值时, ![]() 是等腰三角形,并求出
是等腰三角形,并求出![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,a、b、c 均为非零实数,且 a>b>c,关于 x 的一元二次方程ax2 bx c 0 有两个实数根 x1和 2。(1)4a +2b +c _____0,a _____0,c _________0(填“>”,“=”,“<”)(2)方程 ax2 bx c 0 的另一个根 x1=_______(用含 a、c 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
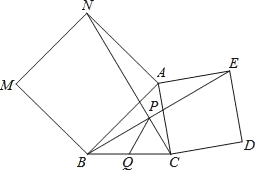
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
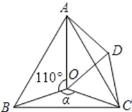
【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)试说明:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当∠BOC为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
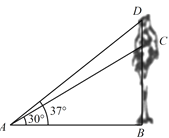
【题目】九(1)班课题学习小组,为了了解大树生长状况,去年在学校门前点 ![]() 处测得一棵大树顶点
处测得一棵大树顶点 ![]() 的仰角为
的仰角为 ![]() ,树高
,树高 ![]() .今年他们仍在原点
.今年他们仍在原点 ![]() 处测得树顶点
处测得树顶点 ![]() 的仰角为
的仰角为 ![]() ,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据:
,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com