
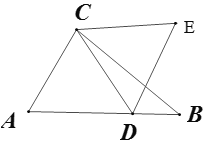
【题目】如图,△ABC中,AB=8,AC=5,BC=7,点D在AB上一动点,线段CD绕点C逆时针旋转60°得到线段CE,AE的最小值为________
【答案】![]()
【解析】
以AC为边作等边△ACF,连接DF,AE,易证△ACE≌△FCD,可得AE=FD,当FD最小时,AE最小,F为定点,D为AB上动点,则FD⊥AB时,FD取得最小值,过C作CM⊥AB于M,过F作FH⊥AB于点H,设AM=x,利用勾股定理解出x=2.5,所以∠CAB=60°,可推出∠FAH=60°,求出FH即为AE的最小值.
解:如图,以AC为边作等边△ACF,连接DF,AE,
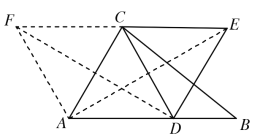
∵线段CD绕点C逆时针旋转60°得到线段CE
∴CE=CD,∠DCE=60°,
∴∠DCE+∠ACD=∠FCA+∠ACD
即∠ACE=∠FCD
在△ACE和△FCD中,
∵AC=FC,∠ACE=∠FCD,CE=CD
∴△ACE≌△FCD(SAS)
∴AE=FD
当FD⊥AB时,FD取得最小值,即为AE的最小值,
如图,过C作CM⊥AB于M,过F作FH⊥AB于点H,
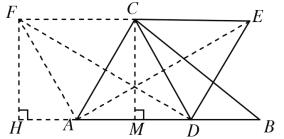
设AM=x,∵AB=8,AC=5,BC=7
∴BM=8-x,
在Rt△ACM和Rt△BCM中,
![]()
∴![]()
解得![]()
∴![]()
∴∠ACM=30°,∠CAM=60°,
∴∠FAH=180°-60°-60°=60°
∴∠AFH=30°,
∴![]() ,
,![]()
∴AE的最小值=FH=![]() .
.
故答案为:![]() .
.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米.甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地. 乙骑行到一半时,发现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地. 已知,乙骑行的总时间是甲步行时间的![]() .设甲步行的时间为
.设甲步行的时间为![]() (分),图中线段OA表示甲离开学校的路程
(分),图中线段OA表示甲离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程
(分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(1)甲步行的速度和乙骑行的速度;
(2)甲出发多少时间后,甲、乙两人第二次相遇?
(3)若![]() (米)表示甲、乙两人之间的距离,当
(米)表示甲、乙两人之间的距离,当![]() 时,求
时,求![]() (米)关于
(米)关于![]() (分)的函数关系式.
(分)的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城镇在对一项工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲队工程款2万元,付乙队工程款1.5万元.现有三种施工方案:(![]() )由甲队单独完成这项工程,恰好如期完工;(
)由甲队单独完成这项工程,恰好如期完工;(![]() )由乙队单独完成这项工程,比规定工期多6天;(
)由乙队单独完成这项工程,比规定工期多6天;(![]() )由甲乙两队
)由甲乙两队![]() 后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为
后,剩下的由乙队单独做,也正好能如期完工.小聪同学设规定工期为![]() 天,依题意列出方程:
天,依题意列出方程:![]() .
.
(1)请将(![]() )中被墨水污染的部分补充出来:________;
)中被墨水污染的部分补充出来:________;
(2)你认为三种施工方案中,哪种方案既能如期完工,又节省工程款?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线l上摆放着三个三角形:△ABC、△HFG、△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
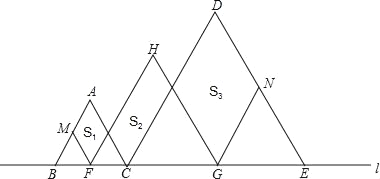
查看答案和解析>>
科目:初中数学 来源: 题型:
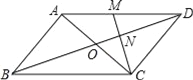
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形(长方形)![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,![]() ,
,![]() 三点在同一直线上,其中正确的是( )
三点在同一直线上,其中正确的是( )
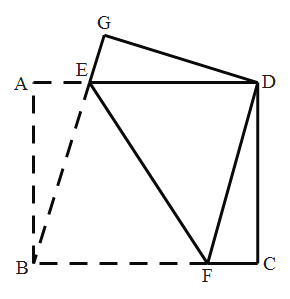
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com