
【题目】如图,将矩形(长方形)![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,![]() ,
,![]() 三点在同一直线上,其中正确的是( )
三点在同一直线上,其中正确的是( )
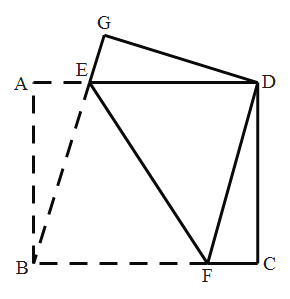
A.①②③B.①③④C.②③④D.①②④
【答案】B
【解析】
根据矩形的对边平行和折叠前后的图形对称的性质,逐项进行分析可得出正确结论.
∵将矩形ABCD沿EF折叠,使点B与点D重合,点A落在点G处,
∴BF=DF,∠BFE=∠EFD,
∵![]() ,
,
∴∠DEF=∠EFB,
∴∠DEF=∠DFE,
∴DE=DF,故①正确;
同理,∠BEF=∠DEF,∠EBF=∠AEB,
∠AEB与∠BEF不一定相等,
∴∠EBF与∠BEF不一定相等,FB与FE不一定相等,故②错误;
![]() ,
,
∵BF=DF,DE=DF,
∴DE=BF,
又∵![]() ,
,
∴四边形BFDE是平行四边形,
∴![]() ,故③正确;
,故③正确;
由矩形可知![]() ,
,
已证四边形BFDE是平行四边形,则有![]() ,
,
∴![]() ,
,![]() ,
,![]() 三点在同一直线上,即④正确;
三点在同一直线上,即④正确;
综上正确的有①③④,
故选:B


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】为提倡绿色出行,某公司在我区![]() 、
、![]() 两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
两个街区分别投放了一批“共享汽车”,“共享汽车”有甲、乙不同款型.
(1)该公司在我区![]() 街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
街区早期试点时共投放甲、乙两种型号的“共享汽车”各20辆,投放成本共计划110万,其中甲型汽车的成本单价比乙型汽车少0.5万元,求甲、乙两型“共享汽车”的单价各是多少?
(2)该公司采取了如下的投放方式: ![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,
辆“共享汽车”,![]() 街区每2000人投放
街区每2000人投放![]() 辆“共享汽车”,按照这种设放方式,
辆“共享汽车”,按照这种设放方式,![]() 街区共投放150辆,
街区共投放150辆,![]() 街区共投放120辆,如果两个街区共有6万人,试求
街区共投放120辆,如果两个街区共有6万人,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8,AC=5,BC=7,点D在AB上一动点,线段CD绕点C逆时针旋转60°得到线段CE,AE的最小值为________
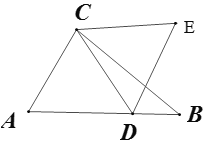
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
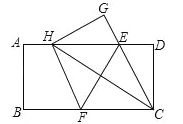
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2![]() .
.
以上结论中,你认为正确的有 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确数字x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.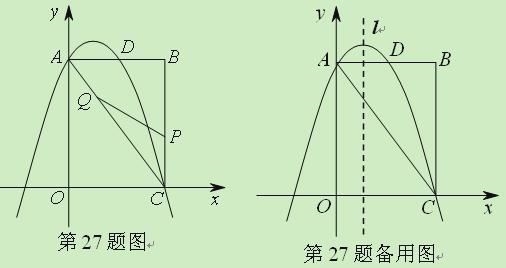
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC的中点为O,点G,H在对角线AC上,AG=CH,直线GH绕点O逆时针旋转α角,与边AB、CD分别相交于点E、F(点E不与点A、B重合).
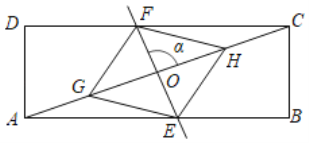
(1)求证:四边形EHFG是平行四边形;
(2)若∠α=90°,AB=9,AD=3,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.
![]() 小明和小刚都在本周日上午去游玩的概率为________;
小明和小刚都在本周日上午去游玩的概率为________;
![]() 求他们三人在同一个半天去游玩的概率.
求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com