
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
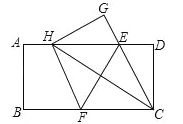
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2![]() .
.
以上结论中,你认为正确的有 .(填序号)
【答案】①③④
【解析】
试题分析:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8﹣x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
则ME=(8﹣3)﹣3=2,
由勾股定理得,
EF=![]() =2
=2![]() ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个,
故答案为①③④.


科目:初中数学 来源: 题型:
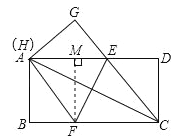
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
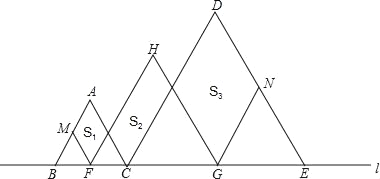
【题目】如图,在直线l上摆放着三个三角形:△ABC、△HFG、△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
CE,F、G分别是BC、CE的中点,FM∥AC∥HG∥DE,GN∥DC∥HF∥AB.设图中三个四边形的面积依次是S1,S2,S3,若S1+S3=20,则S1=_____,S2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
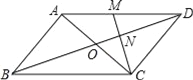
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABNM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
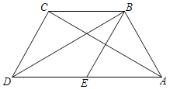
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形(长方形)![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,点
重合,点![]() 落在
落在![]() 处,连接
处,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,
,![]() ,
,![]() 三点在同一直线上,其中正确的是( )
三点在同一直线上,其中正确的是( )
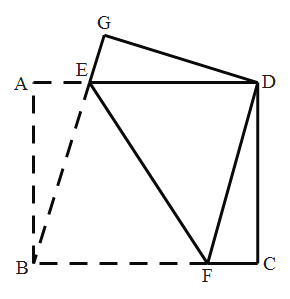
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
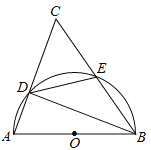
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
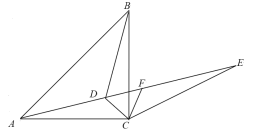
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD.
(1)求证:CD平分∠ACB;
(2)点E是AD延长线上一点,CE=CA,CF∥BD交AE于点F,若∠CAD=15°,
求证:EF=BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com