
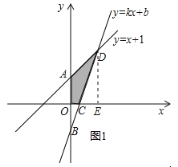
����Ŀ����ͼ����֪���� y=x+1 ��ͼ���� y �ύ�ڵ� A��һ�κ��� y=kx+b ��ͼ���� B��0����1������x �� �Լ� y=x+1 ��ͼ��ֱ��ڵ� C��D���ҵ� D ������Ϊ��1��n����

��1����n= ��k= ��b= ��
��2������ y=kx+b �ĺ���ֵ���ں��� y=x+1 �ĺ���ֵ����X��ȡֵ��Χ�� ��
��3�����ı��� AOCD �������
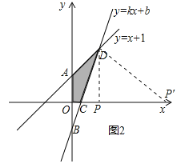
��4���� x�����Ƿ������ P��ʹ���Ե� P��C��D Ϊ�������������ֱ�������Σ������������ P �����ꣻ ������������˵��������
���𰸡���1��2��3��-1����2��![]() ����3��
����3��![]() ��4��
��4��![]() ��
��![]()
��������
�����������1������ֱ��![]() ����
����![]() ���
���![]() ��ֵ��ȷ����A����������B�������
��ֵ��ȷ����A����������B�������![]() �����b��ֵ���ٽ�D�������
�����b��ֵ���ٽ�D�������![]() ���n��ֵ��������D����������
���n��ֵ��������D����������![]() ��ֵ���ɣ�
��ֵ���ɣ�
������һ�κ�������ʽ�����ͼ��ȷ����![]() �ķ�Χ��
�ķ�Χ��
��D��![]() ��ֱ��
��ֱ��![]() �����ı���
�����ı���![]() �������������
�������������![]() �����ȥ������
�����ȥ������![]() �����������ɣ�
�����������ɣ�
��![]() ���ϴ��ڵ�P��ʹ���Ե�P��C��DΪ�������������ֱ�������������ɣ�������������ǣ�
���ϴ��ڵ�P��ʹ���Ե�P��C��DΪ�������������ֱ�������������ɣ�������������ǣ�![]() ��
��![]() ���ֱ����P�����꼴����
���ֱ����P�����꼴����
�����������1������ֱ��![]() ����
����![]() �õ�
�õ�![]() ����A��0��1������B��0��-1������
����A��0��1������B��0��-1������![]() �����ã�
�����ã�![]() ����D��1��n������
����D��1��n������![]() �ã�
�ã�![]() ����D��1��2������D�������
����D��1��2������D�������![]() �еã�
�еã�![]() ����
����![]() ���ʴ�Ϊ��2��3��-1��
���ʴ�Ϊ��2��3��-1��
һ�κ���![]() ��
��![]() ���ڵ�D��1��2������ͼ��ã�����
���ڵ�D��1��2������ͼ��ã�����![]() �ĺ���ֵ���ں���
�ĺ���ֵ���ں���![]() �ĺ���ֵ
�ĺ���ֵ![]() ʱ��ȡֵ��Χ��
ʱ��ȡֵ��Χ��![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
��D��![]() ��ֱ��
��ֱ��![]() ������ͼ1��ʾ����
������ͼ1��ʾ����![]()
![]()
![]()
��4����ͼ2����![]() ���ϴ��ڵ�P��ʹ���Ե�P��C��DΪ�������������ֱ�������������ɣ�������������ǣ���
���ϴ��ڵ�P��ʹ���Ե�P��C��DΪ�������������ֱ�������������ɣ�������������ǣ���![]() ʱ���ɵ�
ʱ���ɵ�![]()
![]() б��Ϊ3��
б��Ϊ3��![]() б��Ϊ
б��Ϊ![]() ��
��![]()
![]() ����ʽΪ
����ʽΪ![]() ��
��![]() ��
��![]() ��
��![]() ʱ����D������Ϊ1���õ�P�������Ϊ1��
ʱ����D������Ϊ1���õ�P�������Ϊ1��![]() ��
��![]() ������
������![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����
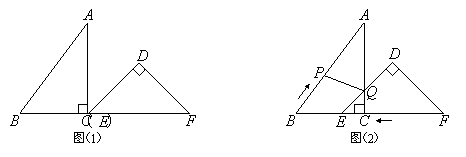
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
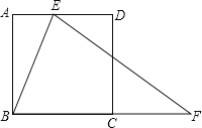
����Ŀ����ͼ��E��������ABCD�ı�AD�ϵĶ��㣬F�DZ�BC�ӳ����ϵ�һ�㣬��BF=EF��AB=12����AE=x��BF=y��
��1������BEF�ǵȱ�������ʱ����BF�ij���
��2����y��x�ĺ�������ʽ����д�����Ķ�����
��3������ABE����ֱ��BE���ۣ���A���ڵ�A��������̽������A��BF�ܷ�Ϊ���������Σ�����ܣ������AE�ij���������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������߶�����ȵ������ε�һ��������߶ΰ������ηֳ�����С������,�������һ���ǵ���������,����һ�������κ�ԭ����������,��ô�������߶ζ���Ϊԭ�����ε�����г�ָ�����.��ͼ,�߶�CD����ABC������г�ָ�����,��ACDΪ����������,��CBD����ABC����,��A=46��,���ACB�Ķ���.
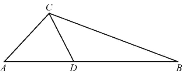
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,AP,CP�ֱ�ƽ�֡�BAC,��ACD,��P=90��,���BAP=��.
(1)������ʾ��ACP;
(2)��֤:AB��CD;
(3)��AP��CF,��֤:FCƽ�֡�DCE.
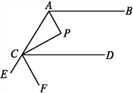
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=90����AC=6��BC=8������P��A���������1cm/s���ٶȣ���A��C��B��B���˶���ͬʱ������Q��C���������2cm/s���ٶȣ���C��B��A��A���˶���������һ���˶����յ�ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��t=_______��ʱ����PCQ���������8cm2.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���C=90�㣬��BAC��ƽ���߽�BC��D����CD=15��AC=30����AB�ij�Ϊ�� ��
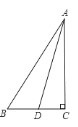
A. 30 B. 40 C. 50 D. 60
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������ABC���������㶼�������η���ĸ����
��1��д��A��B��C��������ꣻ
��2������ABC������ĺ����겻�䣬�����궼����-1������������ϵ�������Ӧ�ĵ�A����B����C���������������������㣬�����õ���A��B��C����ԭ��ABC��������λ�ù�ϵ��
��3���ڣ�2���Ļ����ϣ������궼���䣬�����궼����-1����ͬһ����ϵ�������Ӧ�ĵ�A����B����C���������������������㣬���õ���A��B��C����ԭ��ABC��������λ�ù�ϵ��
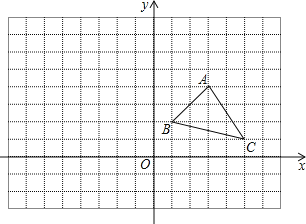
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�B��ʱ����ת���õ���DBE��DE���ӳ�����AC�ཻ�ڵ�F������DA��BF����ABC=��=60�㣬BF=AF��

��1����֤��DA��BC��
��2�������߶�DF��AF��������ϵ����֤����IJ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com