
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
![]() 若
若![]() ,求线段MN的长;
,求线段MN的长;
![]() 若C为线段AB上任一点,满足
若C为线段AB上任一点,满足![]() ,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
![]() 若C在线段AB的延长线上,且满足
若C在线段AB的延长线上,且满足![]() cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
【答案】(1)MN=7cm;(2)MN=![]() a;结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=
a;结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=![]() AB;(3)MN=
AB;(3)MN=![]() b.
b.
【解析】
(1)由中点的定义可得MC、CN长,根据线段的和差关系即可得答案;(2)根据中点定义可得MC=![]() AC,CN=
AC,CN=![]() BC,利用MN=MC+CN,
BC,利用MN=MC+CN,![]() ,即可得结论,总结描述即可;(3)点在AB的延长线上时,根据M、N分别为AC、BC的中点,即可求出MN的长度.
,即可得结论,总结描述即可;(3)点在AB的延长线上时,根据M、N分别为AC、BC的中点,即可求出MN的长度.
(1)∵点M、N分别是AC、BC的中点,AC=8,CB=6,
∴MC=![]() AC=4,CN=
AC=4,CN=![]() BC=3,
BC=3,
∴MN=MC+CN=7cm.
(2)∵点M、N分别是AC、BC的中点,
∴MC=![]() AC,CN=
AC,CN=![]() BC,
BC,
∵AC+BC=AB=a,
∴MN=MC+CN=![]() (AC+BC)=
(AC+BC)=![]() a.
a.
综上可得结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=![]() AB.
AB.
(3)如图:当点C在线段AB的延长线时,则AC>BC,
∵M是AC的中点,
∴CM=![]() AC,
AC,
∵点N是BC的中点,
∴CN=![]() BC,
BC,
∴MN=CM-CN=![]() (AC-BC)=
(AC-BC)=![]() b.
b.
![]()


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
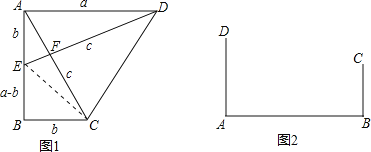
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用代数式表示:
(1)a,b两数的平方和减去它们乘积的2倍;
(2)a,b两数的和的平方减去它们的差的平方;
(3)一个两位数,个位上的数字为a,十位上的数字为b,请表示这个两位数;
(4)若a表示三位数,现把2放在它的右边,得到一个四位数,请表示这个四位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() .说明
.说明![]() 的理由.
的理由.
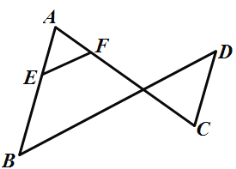
解:∵![]() (已知),
(已知),
∴________//________(_______________)
∴![]() (_______________)
(_______________)
∵![]() (________),
(________),
∴![]() (_______________)
(_______________)
∵![]() (己证),
(己证),
∴![]() (_______________).
(_______________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,沿折线ABCD方向以3cm/s的速度匀速运动;点Q从点D出发,沿线段DC方向以2cm/s的速度匀速运动. 已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为t(s).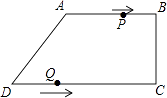
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com