
【题目】如图,已知![]() ,
,![]() .说明
.说明![]() 的理由.
的理由.
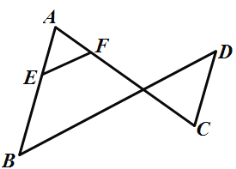
解:∵![]() (已知),
(已知),
∴________//________(_______________)
∴![]() (_______________)
(_______________)
∵![]() (________),
(________),
∴![]() (_______________)
(_______________)
∵![]() (己证),
(己证),
∴![]() (_______________).
(_______________).
【答案】AB,CD,内错角相等,两直线平行,两直线平行,内错角相等,已知,两直线平行,同位角相等,等量代换.
【解析】
根据∠A=∠C可得到AB∥CD,再根据两直线平行,内错角相等可得∠B=∠D,首先根据EF∥BD可得到∠AEF=∠B,再由(1)中证出的∠B=∠D可利用等量代换得到∠AEF=∠D.
解:∵∠A=∠C,(已知)
∴AB∥CD,(内错角相等,两直线平行)
∴∠D=∠B,(两直线平行,内错角相等)
∵EF∥DB,(已知)
∴∠AEF=∠B(两直线平行,同位角相等)
∵∠D=∠B(已证)
∴∠AEF=∠D(等量代换)
故答案为:AB,CD,内错角相等,两直线平行,两直线平行,内错角相等,已知,两直线平行,同位角相等,等量代换.


科目:初中数学 来源: 题型:
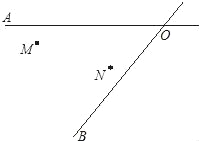
【题目】作图题:(不写作法,但必须保留作图痕迹)
如图:某地有两所大学和两条相交叉的公路,(点M,N表示大学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.
(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
![]() 若
若![]() ,求线段MN的长;
,求线段MN的长;
![]() 若C为线段AB上任一点,满足
若C为线段AB上任一点,满足![]() ,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
![]() 若C在线段AB的延长线上,且满足
若C在线段AB的延长线上,且满足![]() cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90![]() ,射线OC绕点O从OA位置开始,以每秒4
,射线OC绕点O从OA位置开始,以每秒4![]() 的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1
的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1![]() 的速度逆时针方向旋转. 当OC与OA成180
的速度逆时针方向旋转. 当OC与OA成180![]() 时,OC与OD同时停止旋转.
时,OC与OD同时停止旋转.
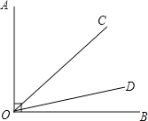
(1)当OC旋转10秒时,∠COD=___.
(2)当OC与OD的夹角是30![]() 时,求旋转的时间.
时,求旋转的时间.
(3)当OB平分∠COD时,求旋转的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是AC上一点,E是AB上一点,且∠AED=∠C.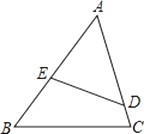
(1)求证:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x,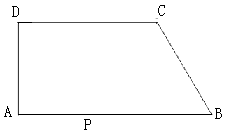
(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)直接写出:当△CDP为等腰三角形时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com