
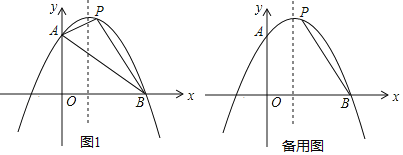
【题目】如图1,已知抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
(1)求这条抛物线的表达式及其顶点坐标;
(2)设点P是抛物线上的动点,若在此抛物线上有且只有三个P点使得△PAB的面积是定值S,求这三个点的坐标及定值S.
(3)若点F是抛物线对称轴上的一点,点P是(2)中位于直线AB上方的点,在抛物线上是否存在一点Q,使得P、Q、B、F为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存请说明理由.
【答案】(1)y=﹣![]() x2+2x+6,顶点坐标为(2,8);(2)点P'(3+3
x2+2x+6,顶点坐标为(2,8);(2)点P'(3+3![]() ,﹣
,﹣![]() ﹣3
﹣3![]() ),P'(3﹣3
),P'(3﹣3![]() ,﹣
,﹣![]() +3
+3![]() ),S=
),S=![]() ;(3)存在,点Q(7,﹣
;(3)存在,点Q(7,﹣![]() )或(﹣1,
)或(﹣1,![]() )或(5,
)或(5,![]() ).
).
【解析】
(1)将交点坐标代入解析式可求解;
(2)设AB上方的抛物线上有点P,过点P作AB的平行线交对称轴于点C,且与抛物线只有一个交点为P,设区PC解析式与抛物线解析式组成方程组,由△=0,可求PC解析式,可求点P坐标,由等底等高的三角形面积相等,可得另两个点所在直线与AB,PC都平行,且与AB的距离等于PC与AB的距离,可求P'E的解析式,即可求解;
(3)分两种情况讨论,由平行四边形的性质可求解.
解:(1)∵抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
∴![]()
∴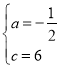
∴抛物线解析式为:y=﹣![]() x2+2x+6,
x2+2x+6,
∵y=﹣![]() x2+2x+6=﹣
x2+2x+6=﹣![]() (x﹣2)2+8,
(x﹣2)2+8,
∴顶点坐标为(2,8)
(2)∵点A(0,6),点B(6,0),
∴直线AB解析式y=﹣x+6,
当x=2时,y=4,
∴点D(2,4)
如图1,设AB上方的抛物线上有点P,过点P作AB的平行线交对称轴于点C,且与抛物线只有一个交点为P,
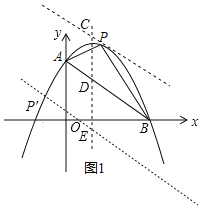
设直线PC解析式为y=﹣x+b,
∴﹣![]() x2+2x+6=﹣x+b,且只有一个交点,
x2+2x+6=﹣x+b,且只有一个交点,
∴△=9﹣4×![]() ×(b﹣6)=0
×(b﹣6)=0
∴b=![]() ,
,
∴直线PC解析式为y=﹣x+![]() ,
,
∴当x=2,y=![]() ,
,
∴点C坐标(2,![]() ),
),
∴CD=![]() ,
,
∵﹣![]() x2+2x+6=﹣x+
x2+2x+6=﹣x+![]() ,
,
∴x=3,
∴点P(3,![]() )
)
∵在此抛物线上有且只有三个P点使得△PAB的面积是定值S,
∴另两个点所在直线与AB,PC都平行,且与AB的距离等于PC与AB的距离,
∴DE=CD=![]() ,
,
∴点E(2,﹣![]() ),
),
设P'E的解析式为y=﹣x+m,
∴﹣![]() =﹣2+m,
=﹣2+m,
∴m=![]()
∴P'E的解析式为y=﹣x+![]() ,
,
∴﹣![]() x2+2x+6=﹣x+
x2+2x+6=﹣x+![]() ,
,
∴x=3±3![]() ,
,
∴点P'(3+3![]() ,﹣
,﹣![]() ﹣3
﹣3![]() ),P'(3﹣3
),P'(3﹣3![]() ,﹣
,﹣![]() +3
+3![]() ),
),
∴S=![]() ×6×(
×6×(![]() ﹣3)=
﹣3)=![]() .
.
(3)设点Q(x,y)
若PB是对角线,
∵P、Q、B、F为顶点的四边形是平行四边形
∴BP与FQ互相平分,
∴![]()
∴x=7
∴点Q(7,﹣![]() );
);
若PB为边,
∵P、Q、B、F为顶点的四边形是平行四边形,
∴BF∥PQ,BF=PQ,或BQ∥FP,BQ=PF,
∴xB﹣xF=xP﹣xQ,或xB﹣xQ=xP﹣xF,
∴xQ=3﹣(6﹣2)=﹣1,或xQ=6﹣(3﹣2)=5,
∴点Q(﹣1,![]() )或(5,
)或(5,![]() );
);
综上所述,点Q(7,﹣![]() )或(﹣1,
)或(﹣1,![]() )或(5,
)或(5,![]() ).
).


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
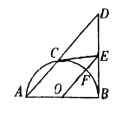
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
科目:初中数学 来源: 题型:
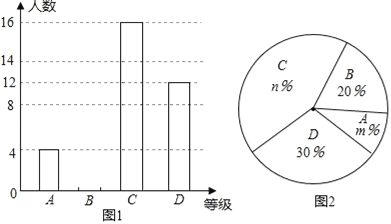
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
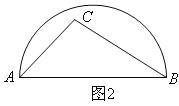
【题目】如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
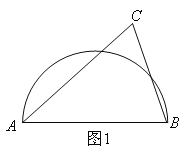
(1)在图1中,画出△ABC的三条高的交点;
(2)在图2中,画出△ABC中AB边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=-x2+mx+m+1(其中m为常数)
(1)该函数的图象与X轴公共点的个数是______个
(2)若该函数的图象的对称轴是直线X=1,顶点为点A,求此时函数的解析式及点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
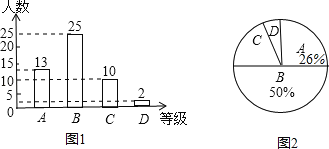
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com