Question

1．如图1，正方形ABCD中，对角线AC、BD相交于点O，点P为BO上一点，PE⊥PA分别交AB于F，交CB的延长线于E点．
（1）求证：PA=PE；
（2）如图2，M、N分别为AE、BC的中点，连接MN、DE，交于点Q，试判断QN和QE的数量关系并证明你的结论；
（3）在图1中，若点F为PE的中点，则tan∠APD的值为3．

Answer 1

分析 （1）过P作PH⊥BC于H、PG⊥AB于G，证得四边形BHPG是正方形，得出PH=PG，再由ASA证得△APG≌△EPH，即可得出结论；
（2）连接OM、BM，OM交DE于F，连接NF，先证明OM是△ACE的中位线，得出OM∥BC，再证明四边形BNFM是平行四边形，得出FN=MB，由SAS证明△MEN≌△FNE，得出对应角相等∠MNE=∠FEN，即可得出结论；
（3）过P作PG⊥AB，交AB于点G，由AAS证得△PGF≌△EBF，得出GF=FB，BE=PG=BG=2GF，由△AGP∽△PGF，得出$\frac{AG}{GP}$=$\frac{GP}{GF}$=2，$\frac{AB}{BG}$=3，证得∠APD=∠AEB，即可求出tan∠APD的值．

解答 （1）证明：过P作PH⊥BC于H、PG⊥AB于G，如图1所示：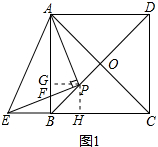
∵四边形ABCD是正方形，
∴∠ABC=90°，∠DBH=45°，
∴四边形BHPG是矩形，△BHP是等腰直角三角形，
∴BH=HP，
∴四边形BHPG是正方形，
∴PH=PG，
∵∠APE=∠APG+∠GPF=90°，∠EPH+∠GPF=90°，
∴∠APG=∠EPH，
在△APG和△EPH中，
$\left\{\begin{array}{l}{∠APG=∠EPH}\\{PH=PG}\\{∠AGP=∠EHP=90°}\end{array}\right.$，
∴△APG≌△EPH（ASA），
∴PA=PE；
（2）解：QN=QE；理由如下：
连接OM、BM，OM交DE于F，连接NF，如图2所示：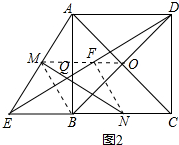
∵四边形ABCD是正方形，
∴OA=OC，AD∥BC，AD=BC，
∵M是AE的中点，
∴OM是△ACE的中位线，
∴OM∥BC，
∴OM∥AD，
∴EF=DF，
∴MF是△ADE的中位线，
∴MF=$\frac{1}{2}$AD，
∴MF=$\frac{1}{2}$BC，
∵N是BC的中点，
∴BN=$\frac{1}{2}$BC，
∴MF=BN，
∴四边形BNFM是平行四边形，
∴FN=MB，
∵∠ABE=90°，
∴MB=$\frac{1}{2}$AE=ME，
∴FN=ME，
即四边形MENF是等腰梯形，
∴∠MEN=∠FNE，
在△MEN和△FNE中，
$\left\{\begin{array}{l}{ME=FN}\\{∠MEN=∠FNE}\\{EN=EN}\end{array}\right.$，
∴△MEN≌△FNE（SAS），
∴∠MNE=∠FEN，
∴QN=QE；
（3）解：∵F为中点，
∴PF=EF，
过P作PG⊥AB，交AB于点G，如图3所示：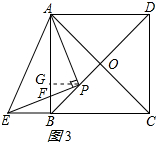
在△PGF和△EBF中，
$\left\{\begin{array}{l}{∠GFP=∠BFE}\\{∠PGF=EBF=90°}\\{PF=EF}\end{array}\right.$，
∴△PGF≌△EBF（AAS），
∴GF=FB，PG=BE，
∵∠PBG=45°，
∴BE=PG=BG=2GF，
∵∠GAP+∠APG=90°，∠GPF+∠APG=90°，
∴∠GAP=∠GPF，
∵∠AGP=∠PGF=90°，
∴△AGP∽△PGF，
∴$\frac{AG}{GP}$=$\frac{GP}{GF}$=2，
∴$\frac{AB}{BG}$=3，
∵△PGF≌△EBF，
∴∠GPF=∠FEB=∠GAP，
∵∠APD=∠GAP+∠ABP=∠GAP+45°，
由（1）得：AP=PE，
∴∠AEP=45°，
∴∠AEB=∠FEB+∠AEP=∠GAP+45°，
∴∠APD=∠AEB，
∴tan∠APD=tan∠AEB=$\frac{AB}{BE}$=$\frac{AB}{BG}$=3．
故答案为：3．

点评 本题是四边形综合题目，考查了正方形的判定与性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、三角形中位线定理、平行四边形的判定与性质、三角函数等知识；本题综合性强，有一定难度，需要通过作辅助线才能得出结论．