
Ζ÷Έω ≈ΉΈοœΏΕΞΒψ ΫΈΣy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©Θ§ΗυΨίΓΑΉσΦ””“ΦθΘ§…œΦ”œ¬ΦθΓ±ΒΡΙφ¬…ΒΟΒΫΤΫ“ΤΚσ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
ΙΊ”Ύx÷αΕ‘≥ΤΒΡΒψΒΡΉχ±ξΒΡΧΊ’ςΘΚΚαΉχ±ξ≤Μ±δΘ§ΉίΉχ±ξΜΞΈΣœύΖ¥ ΐΘΜ
ΙΊ”Ύy÷αΕ‘≥ΤΒΡΒψΒΡΉχ±ξΧΊ’ςΘΚΉίΉχ±ξ≤Μ±δΘ§ΚαΉχ±ξΜΞΈΣœύΖ¥ ΐΘΜ
ΙΊ”Ύ‘≠ΒψΕ‘≥ΤΒΡΒψΒΡΉχ±ξΧΊ’ςΘΚΚαΓΔΉίΉχ±ξΨυΜΞΈΣœύΖ¥ ΐΘ°
Ϋβ¥π ΫβΘΚ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=ax2+bx+c=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©Θ§‘ρΕΞΒψΉχ±ξΈΣΘ®-$\frac{b}{2a}$Θ§$\frac{4ac-{b}^{2}}{4a}$Θ©Θ°
‘ρœρ…œΤΫ“ΤkΘ®kΘΨ0Θ©ΗωΒΞΈΜΚσΒΡΕΞΒψΉχ±ξΈΣΘΚΘ®-$\frac{b}{2a}$Θ§$\frac{4ac-{b}^{2}}{4a}$+kΘ©Θ§Υυ“‘ΤΫ“ΤΚσΒΡΫβΈω ΫΈΣΘΚy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$+kΘ®aΓΌ0Θ©ΘΜ
œρœ¬ΤΫ“ΤkΘ®kΘΨ0Θ©ΗωΒΞΈΜΚσΒΡΕΞΒψΉχ±ξΈΣΘΚΘ®-$\frac{b}{2a}$Θ§$\frac{4ac-{b}^{2}}{4a}$-kΘ©Θ§Υυ“‘ΤΫ“ΤΚσΒΡΫβΈω ΫΈΣΘΚy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$-kΘ®aΓΌ0Θ©ΘΜ
œρΉσΤΫ“ΤhΘ®hΘΨ0Θ©ΗωΒΞΈΜΚσΘ§ΒΡΕΞΒψΉχ±ξΈΣΘΚΘ®-$\frac{b}{2a}$-hΘ§$\frac{4ac-{b}^{2}}{4a}$Θ©Θ§Υυ“‘ΤΫ“ΤΚσΒΡΫβΈω ΫΈΣΘΚy=aΘ®x+$\frac{b}{2a}$+hΘ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©ΘΜ
œρ”“ΤΫ“ΤhΘ®hΘΨ0Θ©ΗωΒΞΈΜΚσΘ§ΒΡΕΞΒψΉχ±ξΈΣΘΚΘ®-$\frac{b}{2a}$+hΘ§$\frac{4ac-{b}^{2}}{4a}$Θ©Θ§Υυ“‘ΤΫ“ΤΚσΒΡΫβΈω ΫΈΣΘΚy=aΘ®x+$\frac{b}{2a}$-hΘ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©ΘΜ
ΙΊ”Ύx÷αΕ‘≥ΤΒΡΫβΈω ΫΈΣΘΚy=-Θ®ax2+bx+cΘ©=-ax2-bx-cΘΜ
ΙΊ”Ύy÷αΕ‘≥ΤΒΡΫβΈω ΫΈΣΘΚy=ax2-bx+cΘΜ
ΙΊ”Ύ‘≠ΒψΕ‘≥ΤΒΡΫβΈω ΫΈΣΘΚy=-ax2+bx-cΘΜ
Ι ¥πΑΗ «ΘΚy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©ΘΜy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$+kΘ®aΓΌ0Θ©ΘΜy=aΘ®x+$\frac{b}{2a}$Θ©2+$\frac{4ac-{b}^{2}}{4a}$-kΘ®aΓΌ0Θ©ΘΜy=aΘ®x+$\frac{b}{2a}$+hΘ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©ΘΜy=aΘ®x+$\frac{b}{2a}$-hΘ©2+$\frac{4ac-{b}^{2}}{4a}$Θ®aΓΌ0Θ©ΘΜy=-ax2-bx-cΘΜy=ax2-bx+cΘΜy=-ax2+bx-cΘ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΆΦœσ”κΦΗΚΈ±δΜΜΘ°”ΟΤΫ“ΤΙφ¬…ΓΑΉσΦ””“ΦθΘ§…œΦ”œ¬ΦθΓ±÷±Ϋ”¥ζ»κΚ· ΐΫβΈω Ϋ«σΒΟΤΫ“ΤΚσΒΡΚ· ΐΫβΈω ΫΘ°


 ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ
ΩΣ–ΡΩλά÷ΦΌΤΎΉς“Β νΦΌΉς“ΒΈςΑ≤≥ωΑφ…γœΒΝ–¥πΑΗ ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗ
ΟϊΧβ―ΒΝΖœΒΝ–¥πΑΗ ΤΎΡ©Φ·ΫαΚ≈œΒΝ–¥πΑΗ
ΤΎΡ©Φ·ΫαΚ≈œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
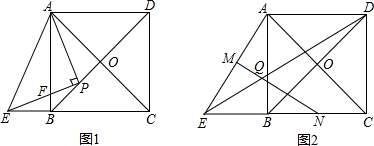
| AΘ° | 13 | BΘ° | $\sqrt{119}$ | CΘ° | 13Μρ$\sqrt{119}$ | DΘ° | ΈόΖ®»ΖΕ® |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
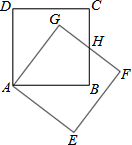 »γΆΦΘ§Α―’ΐΖΫ–ΈABCD»ΤΉ≈ΒψAΘ§Α¥Υ≥ ±’κΖΫœρ–ΐΉΣΒΟΒΫ’ΐΖΫ–ΈAEFGΘ§±ΏFG”κBCΫΜ”ΎΒψHΘ°«σ÷ΛΘΚHC=HFΘ°
»γΆΦΘ§Α―’ΐΖΫ–ΈABCD»ΤΉ≈ΒψAΘ§Α¥Υ≥ ±’κΖΫœρ–ΐΉΣΒΟΒΫ’ΐΖΫ–ΈAEFGΘ§±ΏFG”κBCΫΜ”ΎΒψHΘ°«σ÷ΛΘΚHC=HFΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com